Nondestructive testing for structural defects based on ultrasonic resonance spectroscopy
-
摘要:
超声共振谱是一种利用超声激励样本产生自由振动反演材料力学特性的无损检测方法。首先利用有限元仿真技术研究结构缺陷位置与缺陷大小对超声共振谱及其固有频率的影响,结果表明利用超声共振谱提取的共振频率可以有效判断出结构缺陷所在位置和大小;然后通过试验得到了无缺陷和有缺陷试块的超声共振谱,并进行比较,验证了利用超声共振谱判断结构是否存在缺陷的可行性;最后对有限元仿真所得的超声共振谱与试验所得的超声共振谱进行比较,验证了有限元仿真的准确性。通过仿真和试验研究证明了基于超声共振谱的结构缺陷无损检测方法具有一定的理论和应用价值。
Abstract:Ultrasonic resonance spectroscopy is a nondestructive method used to test materials by generating free vibrations using ultrasonic excitation. This method can be used to determine the mechanical properties of materials. In this article, finite element simulation technology was used to study the impact of structural defects on the ultrasonic resonance spectrum and natural frequency. The results showed that the resonance frequency obtained from the ultrasonic resonance spectrum can determine the location and size of structural defects. In addition, the ultrasonic resonance spectra of test blocks with and without defects were obtained through experimental research. By comparing the two spectra, it was confirmed that ultrasonic resonance spectroscopy can accurately detect structural defects. Finally, the accuracy of finite element simulation was verified by comparing the results with those obtained from experiments. Through simulation and experimental research, it has been proven that ultrasonic resonance spectroscopy is a valuable non-destructive testing method for detecting structural defects.
-
物体的内部缺陷会对结构的力学性能产生显著影响,如何有效检测结构的内部缺陷是相关科研工作者致力研究的目标,国内外的许多学者都在开展有关结构内部缺陷的无损检测研究。常规的无损检测技术包括目视检测、超声检测[1]、射线检测[2]、磁粉检测[3]、涡流检测[4]、渗透检测[5]等。选取合适的无损检测方法可以有效地检测结构的相关物理特性,从而对结构内部是否存在缺陷,以及缺陷的位置和类型进行判别。超声共振谱技术属于超声学的范畴,在20世纪60年代开始得到应用,主要应用于弹性常数的测量。该技术通过超声换能器对结构进行扫频激励,检测出结构的共振频率,在已知结构尺寸、密度的情况下可以反演出材料的弹性常数。当结构的内部存在裂纹或者缺陷时,结构的共振频率就会发生改变,而超声共振谱的共振峰对应的频率即为结构的共振频率,因此超声共振谱可以反映出结构的变化,应用于结构的无损检测。传统的超声检测技术包括超声波脉冲回波和相控阵超声法,而超声共振谱技术目前应用案例较少。目前已有多种获取结构共振谱的方法,如利用激光脉冲[6]、磁场[7]或接触压式电换能器[8]。笔者采用接触式压电换能器来获取共振谱。
文章以铝制立方体结构为研究对象,通过有限元仿真研究结构内部缺陷对固有频率以及超声共振谱的影响,从而证明超声共振谱可以应用于结构的无损检测。并通过试验判断有限元仿真所得到的超声共振谱与试验测得的超声共振谱的一致性,以验证有限元仿真的准确性。最后比较试验测量的有缺陷结构和无缺陷结构的超声共振谱,验证了基于超声共振谱判断结构是否存在缺陷的可行性。
1. 超声共振谱
一个弹性体在自由边界条件下具有多个共振频率,其共振频率本质上为弹性体的固有属性,只依赖于弹性体的几何形状、密度、弹性模量。当弹性体的形状和密度已知的情况下,将待测弹性体的两个对顶角用超声换能器夹住,一侧超声换能器不断更换激励频率进行扫频激励,另一侧超声换能器接收振动信号;扫频完成之后,接收信号的超声换能器将所采集到的信号绘制成超声频谱,这就是弹性体的超声共振谱。当弹性体受到的激励频率与自身固有频率相吻合时,超声换能器会接收到一个幅值较大的信号,其幅值称为共振峰值。因此,通过提取超声共振谱的共振峰值对应的频率便可以得到结构的固有频率。
2. 有限元仿真
2.1 有限元仿真过程
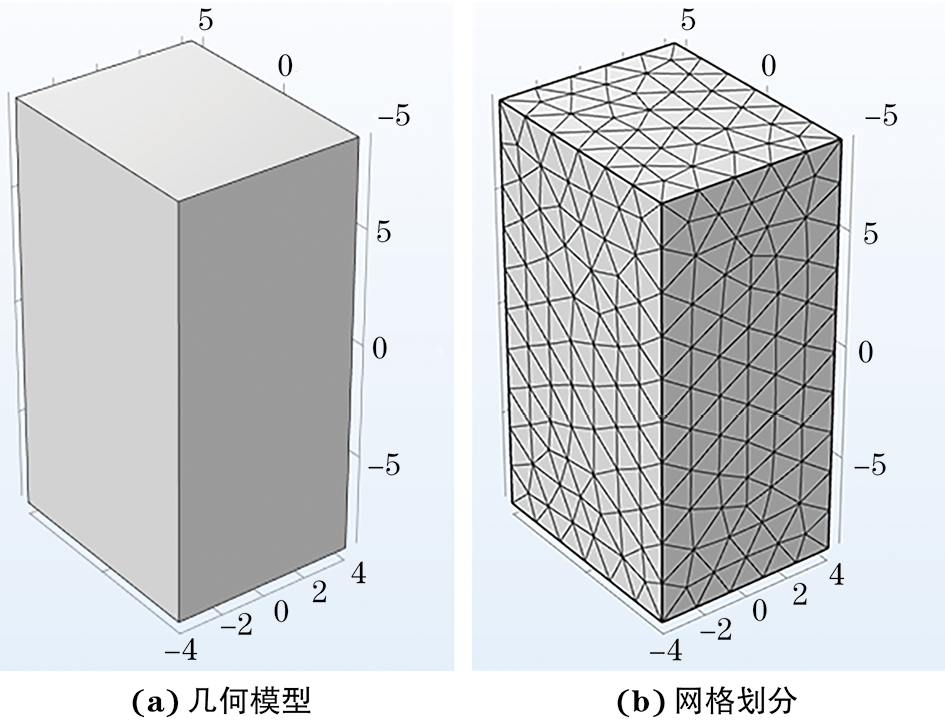
文章采用COMSOL有限元软件进行仿真研究,建立的COMSOL有限元仿真模型如图1所示,如图1(a)所示,首先建立尺寸为8.1 mm×10 mm× 18 mm(长×宽×高)的立方体铝块模型,该尺寸与后续试验中所使用的试件尺寸一致。然后添加材料信息,设置材料参数,并赋予结构相应的材料参数。文章中使用的材料均为铝,铝的杨氏模量为70 GPa,密度2 700 kg·m-3,泊松比为0.33。接下来进行物理场的设置,对于固有频率的仿真,设置为“固体力学场”。根据超声共振谱试验的装置设置,将自由边界应用于结构的所有外表面,结构的中心点采用固定约束。最后对结构进行网格划分,其结果如图1(b)所示。
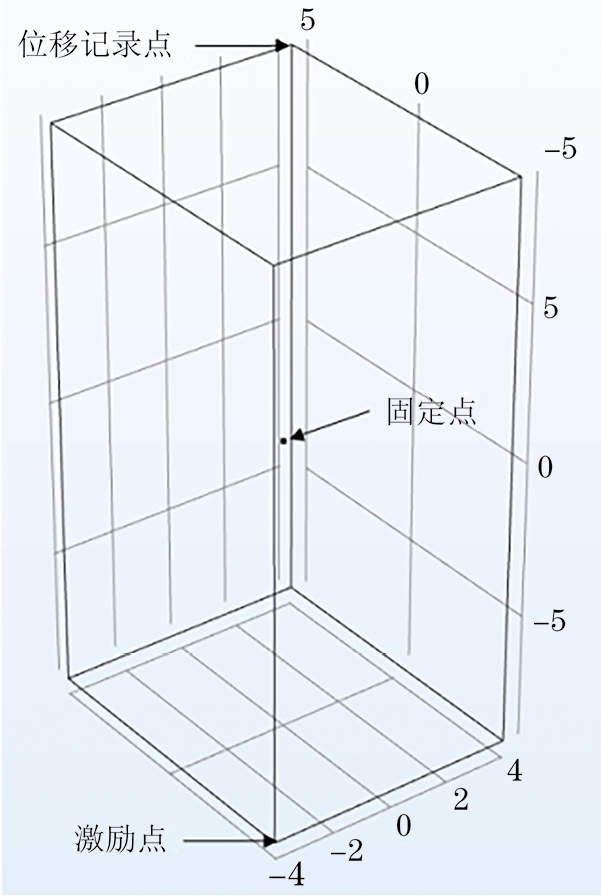
通过COMSOL计算结构的固有频率有两种模式:特征频率模式和频域分析模式。特征频率模式是以某个频率为中心,直接计算该频率附近的固有频率;频域分析模式可以计算出给定频率范围内结构受到激励后,结构位移的完整频谱响应,这和实际情况更为接近。由于试验采取的是对顶角夹持,所以仿真时在立方体铝块的一个顶点(产生激励的超声换能器位置)添加点载荷,记录对顶角(接收信号的超声换能器位置)的位移大小,有限元仿真模型点位设置如图2所示。然后绘制给定频率范围内的频谱图像,峰值所对应的频率即为结构的固有频率。
2.2 结构共振频率的计算
首先利用特征频率模式计算结构的前30阶固有频率。在自由边界条件下计算出的前6阶固有频率为刚性平移和刚性旋转对应的固有频率,故在分析时将其舍去,剩下的前24阶固有频率如表1所示。
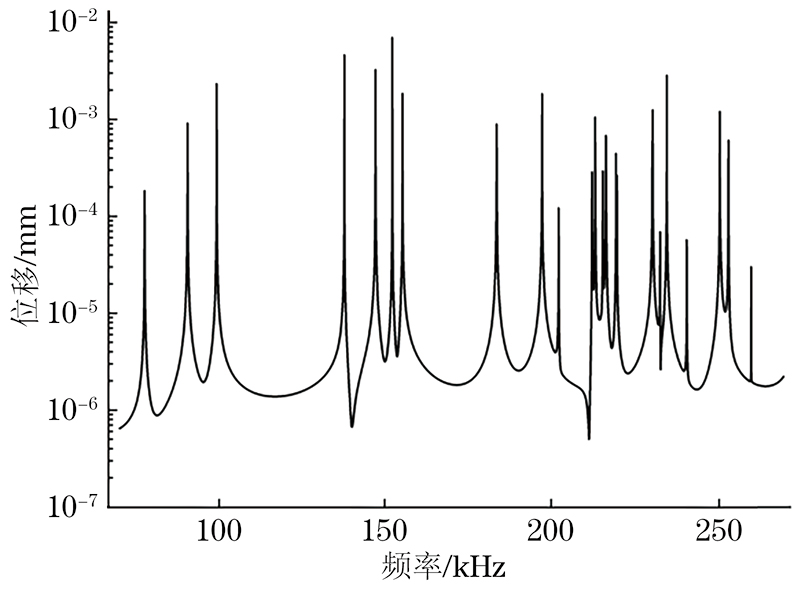
Table 1. 立方体前24阶固有频率阶数 频率/Hz 阶数 频率/Hz 1 77 478 13 214 999 2 87 212 14 215 443 3 96 101 15 219 445 4 137 673 16 219 446 5 147 059 17 230 269 6 152 004 18 230 304 7 155 159 19 231 475 8 183 460 20 234 634 9 197 114 21 240 813 10 199 485 22 250 561 11 212 220 23 250 801 12 213 136 24 258 580 根据表1可知,结构前24阶固有频率分布在70~260 kHz。利用COMSOL的频域分析模式,在70~270 kHz内,以25 Hz为步长进行扫频,取对数后的超声共振谱如图3所示,两种模式计算的固有频率与误差如表2所示。
Table 2. 两种仿真模式计算得到的固有频率与误差阶数 fcal/Hz fRUS/Hz e/% 1 77 478 77 525 0.061 2 87 212 90 450 3.713 3 96 101 99 225 3.251 4 137 673 137 675 0.001 5 147 059 147 075 0.011 6 152 004 152 125 0.080 7 155 159 155 200 0.026 8 183 460 183 575 0.063 9 197 114 197 250 0.069 10 199 485 202 250 1.386 11 212 220 212 275 0.026 12 213 136 213 250 0.053 13 214 999 215 550 0.256 14 215 443 216 525 0.502 15 219 445 219 525 0.036 16 219 466 219 825 0.164 17 230 269 230 400 0.057 18 230 304 230 600 0.129 19 231 475 232 825 0.583 20 234 634 234 825 0.081 21 240 813 240 825 0.005 22 250 561 250 800 0.095 23 250 801 253 400 1.036 24 258 580 260 225 0.636 根据超声共振谱的共振峰提取对应的固有频率fRUS。共振谱提取的固有频率fRUS与特征频率模式计算的固有频率fcal的误差为
(1) 根据表2可知,大部分固有频率对于边界条件不太敏感,通过超声共振谱提取的固有频率与直接计算的固有频率偏差小于0.1%,但纯弯曲模态和压弯复合模态对边界条件较为敏感,误差会达到3%左右。因此,可以利用超声共振谱有效地提取结构的固有频率。
2.3 缺陷位置对超声共振谱的影响
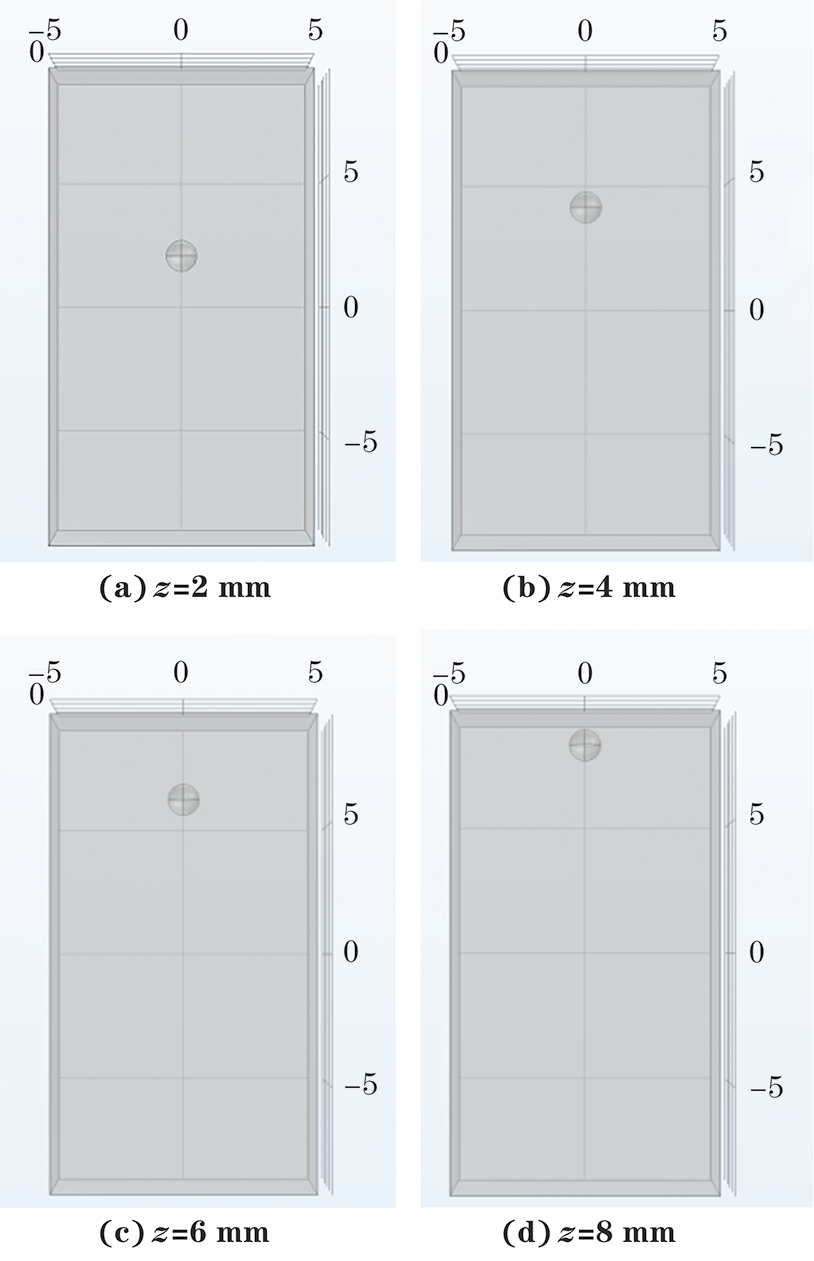
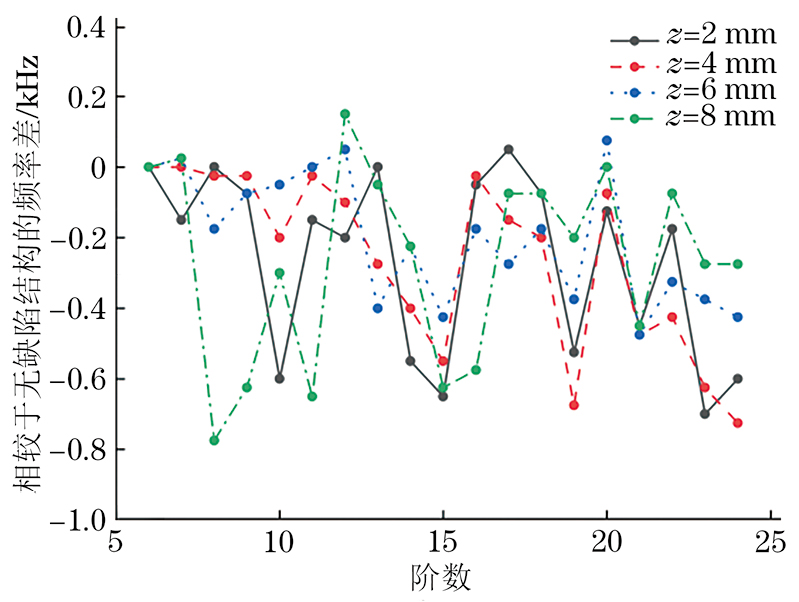
由于利用超声共振谱测量法的前5阶固有频率相较于实际固有频率通常有较大偏差[9],根据表2也可以看出利用超声共振谱测量的第2、3阶固有频率相较于直接计算的固有频率有较大偏差,所以在分析时舍去前5阶固有频率。出现这种偏差有可能是支架-试件耦合所致[10],即前文所提到的边界条件的影响。为了研究缺陷位置对超声共振谱的影响,对具有不同位置缺陷的结构进行仿真,得到各结构的超声共振谱,并与无缺陷结构的超声共振谱进行比较。将缺陷的形状设置为半径0.6 mm的球体,以铝块的中心为原点,设置一系列不同位置的缺陷,缺陷的位置信息及不同缺陷的几何模型如表3和图4所示。
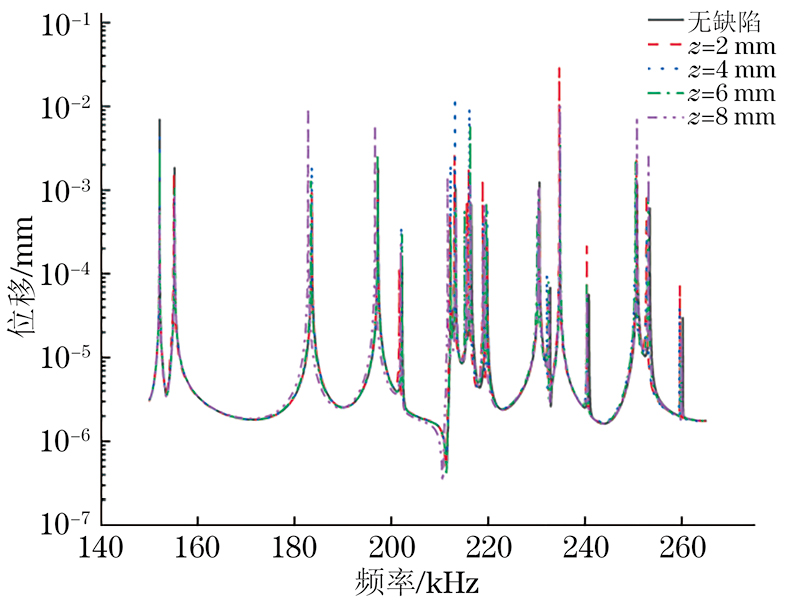
Table 3. 各缺陷的位置信息编号 方向 x y z 缺陷1 0 0 2 缺陷2 0 0 4 缺陷3 0 0 6 缺陷4 0 0 8 用COMSOL频域分析模式计算频率为150~265 kHz的超声共振谱。不含缺陷和含有不同位置缺陷结构的超声共振谱(取对数后)如图5所示。由于超声共振谱的频域范围很广,很难直接观察出不同结构的超声共振谱共振峰的偏移情况,故通过超声共振谱提取出每个结构的第6~24阶固有频率。并计算含缺陷结构与不含缺陷结构的同一阶固有频率的差值。存在不同位置缺陷结构与无缺陷结构的第6~24阶固有频率差值曲线如图6所示。存在不同位置缺陷结构与无缺陷结构的第7~14阶固有频率的差值随模态阶数的变化情况如表4所示,表中↑表示该阶差值比前一阶差值大,↓表示该阶差值比前一阶差值小,-表示该阶差值与前一阶差值一致。根据图6和表4可以看出,缺陷位于不同位置时,存在相同大小缺陷结构与无缺陷结构的第6~24阶固有频率的差值随模态阶数变化的趋势不同,故可以根据固有频率差值随模态阶数的变化趋势确定缺陷所在位置。
Table 4. 存在不同位置缺陷结构与无缺陷结构的固有频率差值变化情况z/mm 阶数 7 8 9 10 11 12 13 14 2 ↓ ↑ ↓ ↓ ↑ ↓ ↑ ↓ 4 - ↓ - ↓ ↑ ↓ ↓ ↓ 6 ↑ ↓ ↑ ↑ ↑ ↑ ↓ ↓ 8 ↑ ↓ ↑ ↑ ↓ ↑ ↓ ↓ 2.4 缺陷大小对超声共振谱的影响
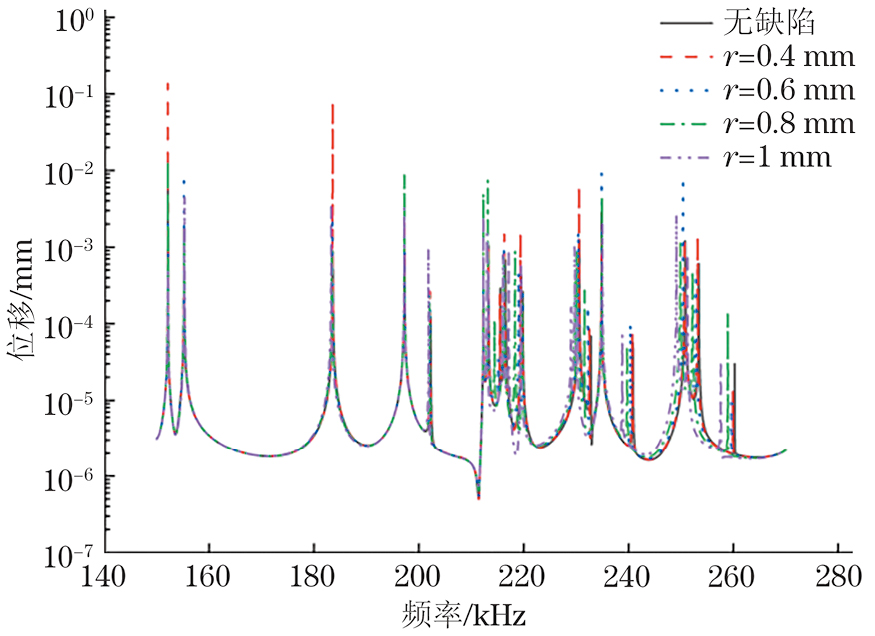
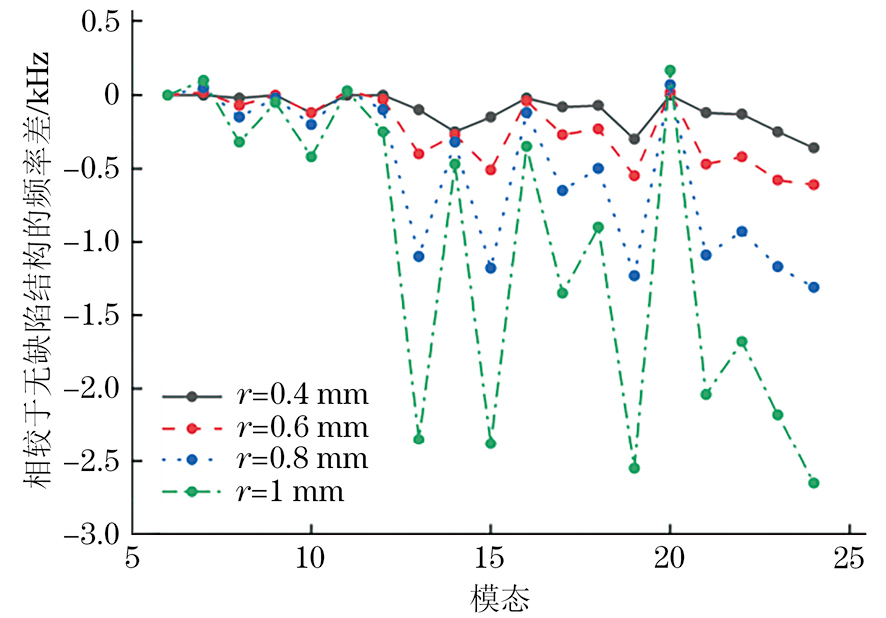
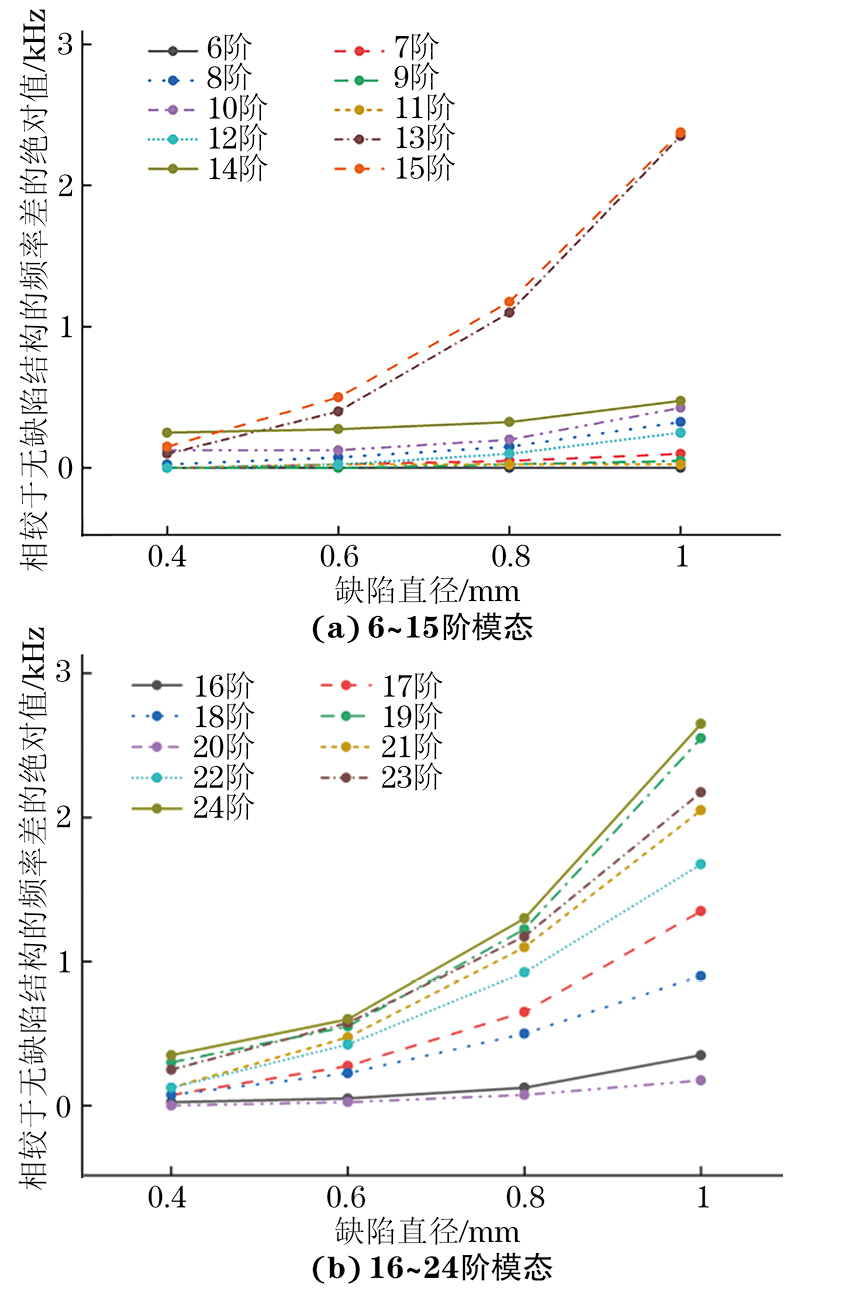
为了研究缺陷大小对超声共振谱的影响,对具有不同大小缺陷的结构进行仿真,得到各结构的超声共振谱,并与无缺陷结构的超声共振谱进行比较。以铝块中心为原点,缺陷中心位于x=0 mm,y=0 mm,z=5 mm处,将缺陷形状设置为半径(r)0.4,0.6,0.8,1 mm的球体,不同大小缺陷的几何模型如图7所示。无缺陷结构和存在不同大小缺陷的结构取对数后的超声共振谱如图8所示。存在不同大小缺陷结构与无缺陷结构的第6~24阶固有频率差值如图9所示。由图9可以观察出,当缺陷在同一位置时,存在不同大小缺陷结构与无缺陷结构的第6~24阶固有频率的差值随模态阶数变化的趋势相似。此外根据图9还可以观察出,同一位置的缺陷直径越大,含缺陷结构与无缺陷结构的同一阶固有频率的差值的绝对值越大,不同大小缺陷结构的6~24阶模态固有频率差值曲线如图10所示,由图10可以更为清晰地观察出此规律。
结合2.3节中结论可知:可以首先通过含缺陷结构的固有频率与无缺陷结构的固有频率的差值随模态阶数的变化趋势来判断结构缺陷的所在位置,再根据含缺陷结构的固有频率与无缺陷结构的固有频率的差值来判断缺陷的大小,从而定位缺陷的位置与大小。故通过超声共振谱来判断结构缺陷的位置与大小具有可行性。
3. 试验验证
3.1 试验方案与仪器
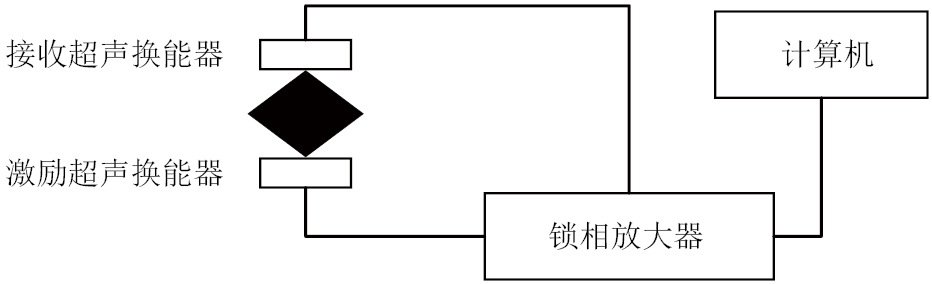
超声共振谱试验装置结构示意如图11所示。试验装置包括激励超声换能器、接收超声换能器、锁相放大器、超声换能器支架与夹具。将制备的立方体试块对角夹持在激励超声换能器和接收超声换能器之间,通过锁相放大器向激励换能器输入扫频正弦信号,接收换能器接收扫频激励下的试块位移响应信号,并输出到锁相放大器中。当输入的激励信号接近试块的固有频率时,接收超声换能器接收到的信号幅值会明显增大,由此检测出试块的固有频率。
3.2 试块结构与尺寸
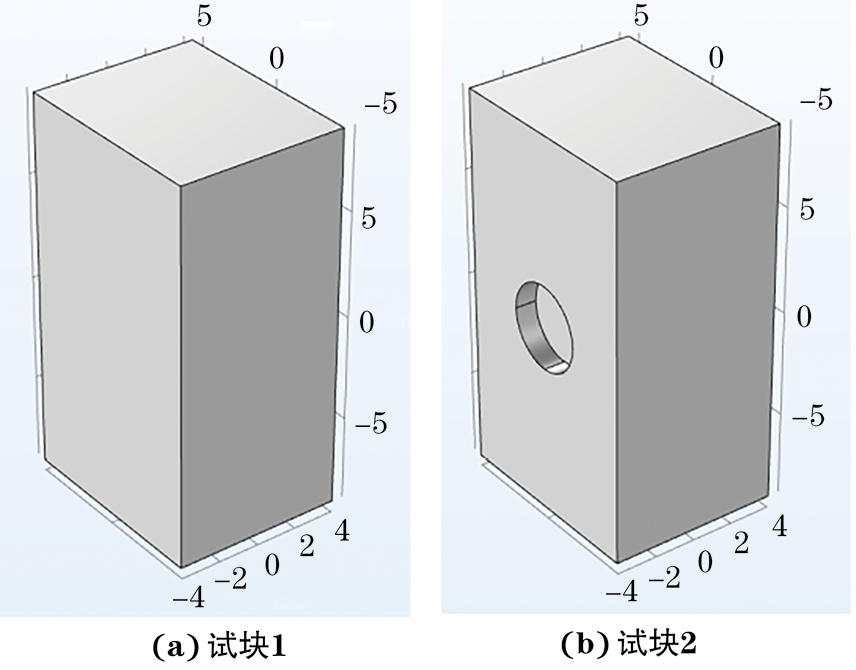
试块1和试块2的材料均为铝,尺寸均为8.1 mm×10 mm×18 mm(长×宽×高),其中试块1没有缺陷,试块2在10 mm×18 mm的表面中心存在一个半径为2 mm,深度为1 mm的圆柱形缺陷。试块1,2的几何模型如图12所示。
3.3 试验数据和结果分析
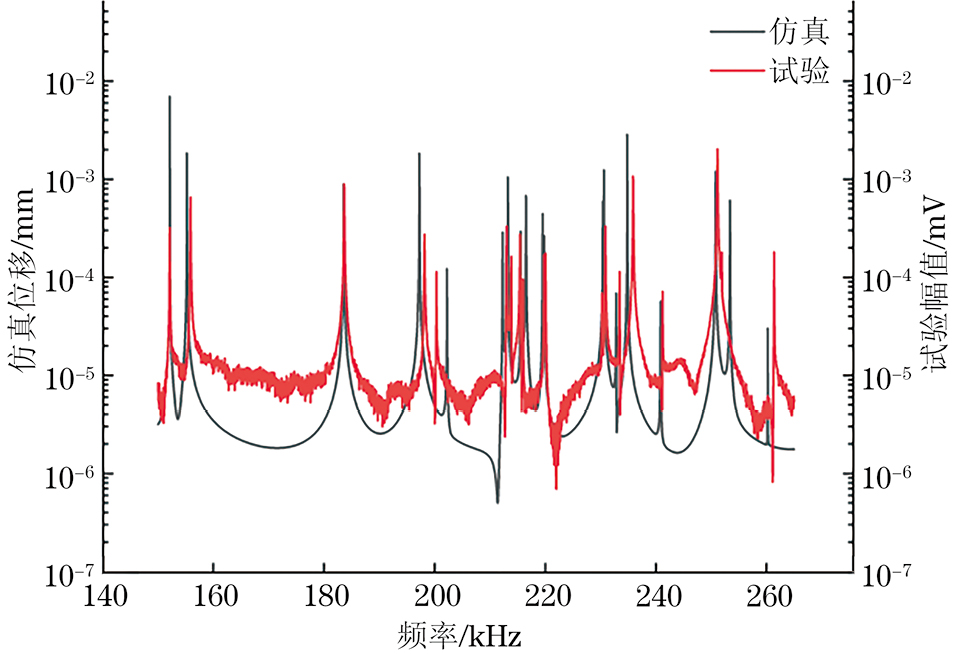
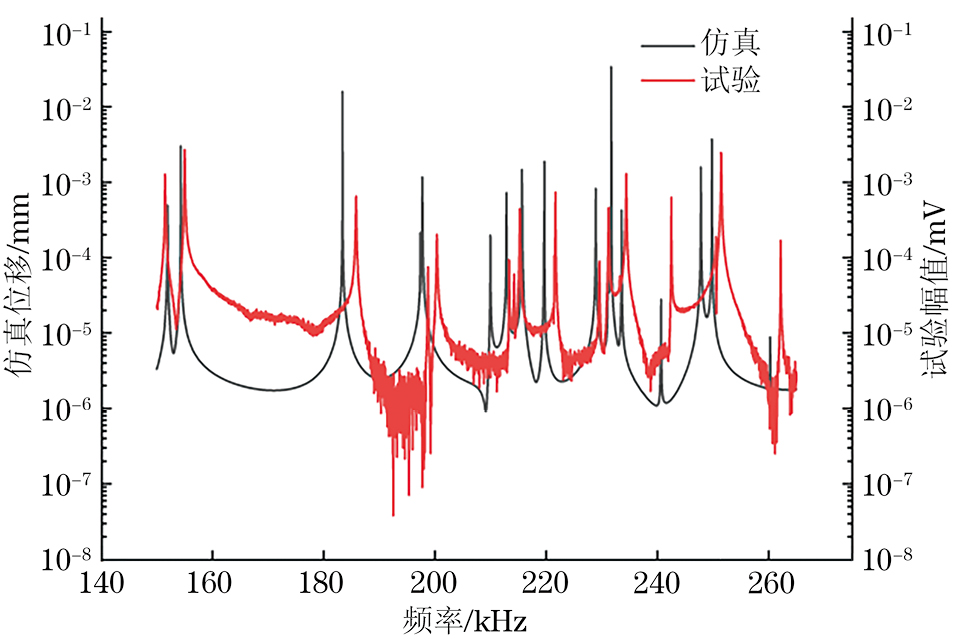
利用搭建好的设备测量试块1,2的超声共振谱。测量试块1,2所得的超声共振谱与有限元仿真所得的超声共振谱如图13,14所示,频域为150~270 kHz。
观察图13可以发现,测量试块1所得与有限元仿真所得的超声共振谱的大部分共振峰都是较为吻合的,但也存在一些有较大偏差的共振峰。观察图14可以发现,测量试块2所得与有限元仿真所得的超声共振谱的共振峰均存在明显偏差,试验所得的共振峰相较于仿真所得的共振峰整体向右发生了偏移,但是两者整体规律是一致的。
试验测量与有限元仿真所得的超声共振谱的误差来源主要有以下几方面。
(1) 试块加工精度不高,导致试块的结构不够规则,是误差的主要来源。
(2) 试块的材料属性与有限元仿真中设置的材料属性存在差异。
(3) 实际的边界条件与有限元仿真设置的边界条件存在差异。
为了更细致地研究试验所得与有限元仿真所得超声共振谱的差异,根据试验所得超声共振谱提取试块的固有频率ftest,同时提取有限元仿真得到的超声共振谱中的固有频率fsim,并计算ftest相较于fsim的误差,即
(2) 试块1仿真与测试所得的固有频率误差如表5,6所示。根据表5,6可知,试验所得到的超声共振谱提取出的固有频率相较于有限元仿真结果中提取出的固有频率,误差大部分在1%以内,验证了有限元仿真得到的超声共振谱的准确性,故通过有限元仿真研究所得的结论也具有准确性。
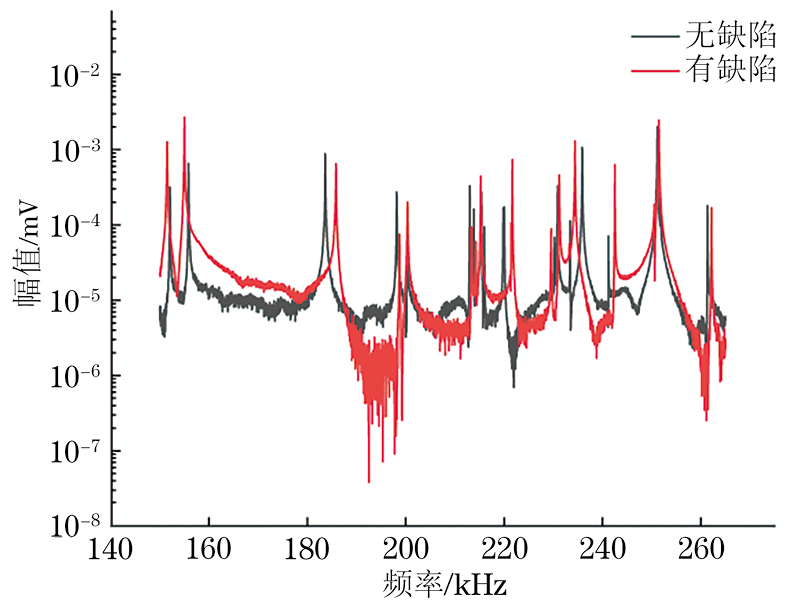
Table 5. 试块1仿真与测试所得的固有频率误差阶数 fsim/Hz ftest/Hz e/% 6 152 125 152 225 0.066 7 155 200 155 950 0.483 8 183 575 183 825 0.136 9 197 250 198 350 0.558 10 202 250 200 375 -0.927 11 212 275 213 050 0.365 12 213 250 213 925 0.317 13 215 550 215 475 -0.035 14 216 525 216 000 -0.242 15 219 525 219 825 0.137 16 219 825 220 100 0.125 17 230 400 230 325 -0.033 18 230 600 230 950 0.152 19 232 825 233 400 0.247 20 234 825 235 925 0.468 21 240 825 241 175 0.145 22 250 800 251 175 0.150 23 253 400 252000 -0.552 24 260 225 261 300 0.413 Table 6. 试块2仿真与测试所得的固有频率误差阶数 fsim/Hz ftest/Hz e/% 6 151 925 151 500 -0.280 7 154 300 155 025 0.470 8 183 400 185 825 1.322 9 197 350 198 750 0.709 10 197 725 200 350 1.328 11 209 950 213 350 1.619 12 212 850 214 275 0.669 13 215 625 215 250 -0.174 14 215 700 215 375 -0.151 15 219 575 221 450 0.854 16 219 675 221 675 0.910 17 228 925 229 575 0.284 18 231 150 231 225 0.032 19 231 700 233 225 0.658 20 233 550 234 400 0.364 21 240 650 242 500 0.769 22 247 825 250 525 1.089 23 249 800 251 450 0.661 24 260 275 262 150 0.720 测量试块1,2所得的超声共振谱如图15所示,可见,当结构存在缺陷时,超声共振谱的共振峰相对于无缺陷结构的共振峰有明显偏移,说明结构缺陷确实会对超声共振谱产生影响,通过超声共振谱来判断结构是否存在缺陷是可行的。
4. 结语
(1) 通过COMSOL有限元仿真的特征频率模式计算了结构自由振动的固有频率,通过频域分析模式仿真得到了超声共振谱,并提取了共振峰对应的频率,将两组频率进行比较,证明超声共振谱能有效提取结构的固有频率。
(2) 通过COMSOL有限元仿真的频域分析模式仿真得到了立方体铝块的超声共振谱,研究了当结构存在缺陷时固有频率的变化,结果表明,当缺陷位于不同位置时,存在相同大小缺陷结构的固有频率与无缺陷结构的固有频率的差值随模态阶数变化的趋势不同;当缺陷位于相同位置时,存在不同大小缺陷结构的固有频率与无缺陷结构的固有频率的差值随模态阶数变化的趋势相似;当缺陷位于相同位置时,缺陷越大,含缺陷结构与无缺陷结构的同一阶固有频率的差越大。故,可以通过超声共振谱来判断缺陷位置与大小。
(3) 通过试验测量得到了无缺陷和有缺陷试块的超声共振谱,并与有限元仿真得到的超声共振谱进行比较,验证了有限元仿真获得的超声共振谱的准确性。
(4) 通过试验测量得到的无缺陷和有缺陷试块的超声共振谱共振峰存在明显差异,验证了超声共振谱可以用于判断结构是否存在缺陷的结论。
本文获“2024 Evident杯超声检测技术优秀论文评选”活动三等奖。 -
Table 1 立方体前24阶固有频率
阶数 频率/Hz 阶数 频率/Hz 1 77 478 13 214 999 2 87 212 14 215 443 3 96 101 15 219 445 4 137 673 16 219 446 5 147 059 17 230 269 6 152 004 18 230 304 7 155 159 19 231 475 8 183 460 20 234 634 9 197 114 21 240 813 10 199 485 22 250 561 11 212 220 23 250 801 12 213 136 24 258 580 Table 2 两种仿真模式计算得到的固有频率与误差
阶数 fcal/Hz fRUS/Hz e/% 1 77 478 77 525 0.061 2 87 212 90 450 3.713 3 96 101 99 225 3.251 4 137 673 137 675 0.001 5 147 059 147 075 0.011 6 152 004 152 125 0.080 7 155 159 155 200 0.026 8 183 460 183 575 0.063 9 197 114 197 250 0.069 10 199 485 202 250 1.386 11 212 220 212 275 0.026 12 213 136 213 250 0.053 13 214 999 215 550 0.256 14 215 443 216 525 0.502 15 219 445 219 525 0.036 16 219 466 219 825 0.164 17 230 269 230 400 0.057 18 230 304 230 600 0.129 19 231 475 232 825 0.583 20 234 634 234 825 0.081 21 240 813 240 825 0.005 22 250 561 250 800 0.095 23 250 801 253 400 1.036 24 258 580 260 225 0.636 Table 3 各缺陷的位置信息
编号 方向 x y z 缺陷1 0 0 2 缺陷2 0 0 4 缺陷3 0 0 6 缺陷4 0 0 8 Table 4 存在不同位置缺陷结构与无缺陷结构的固有频率差值变化情况
z/mm 阶数 7 8 9 10 11 12 13 14 2 ↓ ↑ ↓ ↓ ↑ ↓ ↑ ↓ 4 - ↓ - ↓ ↑ ↓ ↓ ↓ 6 ↑ ↓ ↑ ↑ ↑ ↑ ↓ ↓ 8 ↑ ↓ ↑ ↑ ↓ ↑ ↓ ↓ Table 5 试块1仿真与测试所得的固有频率误差
阶数 fsim/Hz ftest/Hz e/% 6 152 125 152 225 0.066 7 155 200 155 950 0.483 8 183 575 183 825 0.136 9 197 250 198 350 0.558 10 202 250 200 375 -0.927 11 212 275 213 050 0.365 12 213 250 213 925 0.317 13 215 550 215 475 -0.035 14 216 525 216 000 -0.242 15 219 525 219 825 0.137 16 219 825 220 100 0.125 17 230 400 230 325 -0.033 18 230 600 230 950 0.152 19 232 825 233 400 0.247 20 234 825 235 925 0.468 21 240 825 241 175 0.145 22 250 800 251 175 0.150 23 253 400 252000 -0.552 24 260 225 261 300 0.413 Table 6 试块2仿真与测试所得的固有频率误差
阶数 fsim/Hz ftest/Hz e/% 6 151 925 151 500 -0.280 7 154 300 155 025 0.470 8 183 400 185 825 1.322 9 197 350 198 750 0.709 10 197 725 200 350 1.328 11 209 950 213 350 1.619 12 212 850 214 275 0.669 13 215 625 215 250 -0.174 14 215 700 215 375 -0.151 15 219 575 221 450 0.854 16 219 675 221 675 0.910 17 228 925 229 575 0.284 18 231 150 231 225 0.032 19 231 700 233 225 0.658 20 233 550 234 400 0.364 21 240 650 242 500 0.769 22 247 825 250 525 1.089 23 249 800 251 450 0.661 24 260 275 262 150 0.720 -
[1] 付宗周. 碳纤维复合材料孔隙率超声检测与评价[J].无损检测,2023,45(9):33-38,73. [2] 张林文,朱妍,朱毅. X射线数字成像技术在预应力索灌浆质量检测中的应用[J].无损检测,2023,45(1):20-22. [3] 朱欣欣. 道岔钢轨制造中磁粉检测的常见缺陷分析[J].无损检测,2020,42(6):68-69,72. [4] 苗堃,张胜利,陈垒,等. 高压电缆铅封附件缺陷的涡流检测[J].无损检测,2023,45(9):17-21. [5] 刘步良,李诚,徐培良,等. 余热排出热交换器管板焊缝的渗透检测[J].无损检测,2021,43(9):69-72. [6] HURLEY D H ,REESE S J ,PARK S K ,et al .In situ laser-based resonant ultrasound measurements of microstructure mediated mechanical property evolution[J].2010,107(6):063510. [7] SCHWARZ R B ,VUORINEN J F .Resonant ultrasound spectroscopy:applications,current status and limitations[J].Journal of Alloys and Compounds,2000,310(1):243-250. [8] MIGLIORI A ,SARRAO J L ,VISSCHER W M ,et al .Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids[J].Physica B:Condensed Matter,1993,183(1):1-24. [9] CHIMENTI D E. Resonant ultrasound spectroscopy: applications to physics, materials measurements, and nondestructive evaluation: a migliori and JL Sarrao[J].Applied Mechanics Reviews,1999, 52: 14. [10] YONEDA A .Intrinsic eigenvibration frequency in the resonant ultrasound spectroscopy:evidence for a coupling vibration between a sample and transducers[J].Earth,Planets and Space,2002,54(7):763-770.



 下载:
下载: