Whole Service Life Prediction of Concrete Reinforced Construction under Multi-Factors Action in Marine Environment
-
摘要:
基于现代混凝土技术的发展,即使钢筋周围混凝土中的Cl-含量达到临界值,仍可有效延缓钢筋的腐蚀发展,定义海洋环境钢筋混凝土构筑物的全寿命T为钢筋腐蚀诱导阶段t0和腐蚀发展阶段t1之和。分别对t0、t1进行模型预测。在t0阶段,基于Fick第二定律,考虑混凝土对Cl-结合、Cl-扩散时间依赖性与材料缺陷、劣化等对Cl-扩散性影响,建立多因素影响的混凝土Cl-扩散模型。采用反函数等严密推导该模型,计算了保护层厚度达到钢筋开始锈蚀的临界Cl-含量所需时间。在t1阶段,基于弹性与断裂力学,考虑钢筋与混凝土界面间隙层对初期锈胀的缓冲,计算了锈蚀膨胀使钢筋与保护层组成的环状筒体达到其极限拉应力所需的径向临界锈胀应力,预测了产生该锈胀应力所需时间。
Abstract:The advancement of contemporary concrete technology allows for the effective delaying of the corrosion development of steel bars, even in cases where the concentration of Cl- in the concrete surrounding them reaches a critical level. The total of the steel bar corrosion induction stage (t0) and the corrosion development stage (t1) is the whole life T of reinforced concrete structures in marine conditions. Model predictions were made for t0 and t1 respectively. At the t0 stage, a multi-factor concrete Cl- diffusion model was established based on Fick's second law, taking into account the effects of concrete on Cl- binding, Cl- diffusion time dependence, material defects, deterioration, and other factors on Cl- diffusion. The inverse function for the model was rigorously derived to determine how long it would take for the protective layer thickness to reach the critical Cl- concentration at which the steel bars started to corrode. The radial critical rust expansion stress needed for the annular cylinder made of steel bars and protective layer to reach its ultimate tensile stress due to rust expansion was calculated at stage t1 based on elasticity and fracture mechanics, taking into account the buffering effect of the interface gap layer between steel bars and concrete on initial rust expansion. The amount of time needed to produce this rust expansion stress was predicted using Faraday's equation.
-
Keywords:
- concrete /
- life prediction /
- corrosion /
- chloride /
- diffusion /
- initiation time /
- propagation time
-
海洋环境中的Cl-通过混凝土保护层迁移渗透到钢筋表面引起钢筋锈蚀破坏,是导致海洋环境钢筋混凝土构筑物破坏的最主要原因。据调查,我国20世纪90年代前兴建的海港工程一般使用10~20 a就出现严重的钢筋锈蚀,使用寿命远远不能达到构筑物的设计基准期,这给国家带来巨大经济损失。基于此,许多学者开始对海洋环境中钢筋混凝土构筑物的使用寿命预测进行研究,提出许多预测模型并将其应用于实际工程。文献[1]总结评价了几种混凝土构筑物的使用寿命预测模型,并分别指出其优缺点及适用范围。
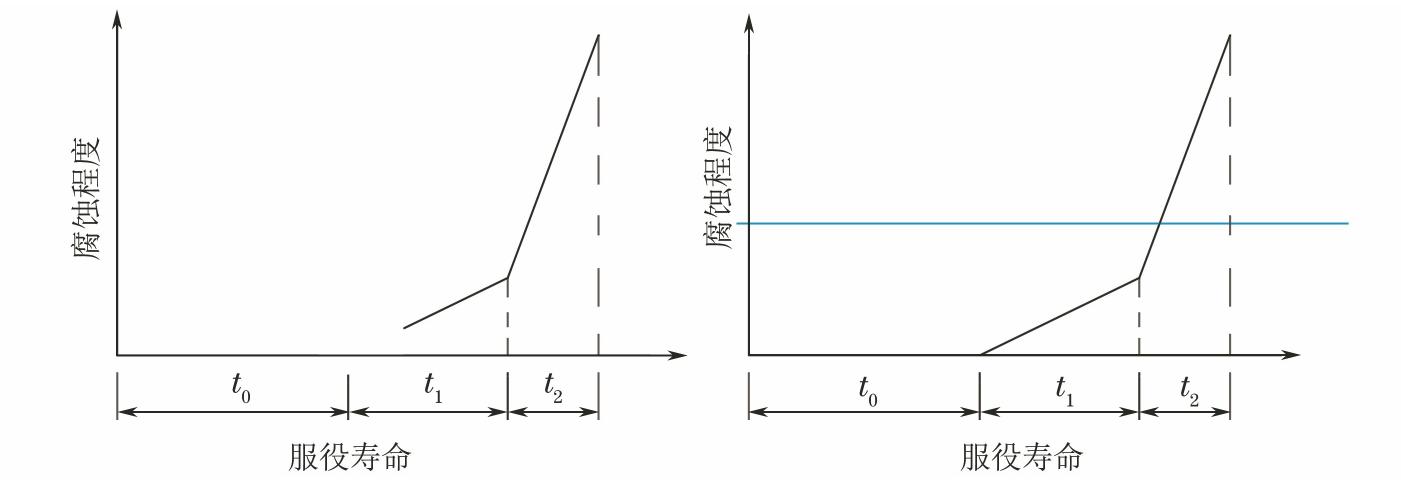
钢筋混凝土构筑物的服役寿命一般分为3阶段[2-3]:钢筋腐蚀诱导阶段t0,腐蚀发展阶段t1,腐蚀破坏阶段t2,如图1所示。
(1)腐蚀诱导阶段 构筑物暴露于海洋环境后,具有很强穿透力的Cl-逐渐向混凝土内部入侵积聚;当Cl-含量到达临界含量时,Cl-破坏钝化膜并激活表面铁原子,钢筋开始锈蚀。t0为钢筋周围混凝土中Cl-达到钢筋临界锈蚀含量所经历的时间。该段时间与混凝土抗Cl-渗透性、环境有关。
(2)腐蚀发展阶段 钢筋开始锈蚀后,在氧气、水供应充足的条件下,电化学腐蚀顺利进行,腐蚀产物体积增加,产生锈胀应力,当锈胀应力大于混凝土极限拉应力时,保护层开裂。该段时间与钢筋直径、氧气和水在钢筋混凝土中的扩散速率、混凝土电阻率等有关。Cl-在腐蚀反应中起催化和去极化作用,没被消耗;一旦Cl-含量超过临界值,若不采取措施,腐蚀将不断进行。
(3)腐蚀破坏阶段 保护层开裂后,钢筋直接与氯盐接触,腐蚀急剧加快;保护层被胀裂甚至脱落,钢筋截面大幅减小,结构承载力降低,无法满足安全使用功能。
目前国内外[4-5]关于构筑物的服役寿命一般定义为腐蚀诱导阶段,寿命预测的研究也主要集中于该阶段。但随着现代高抗渗的高性能混凝土、迁移渗透型阻锈剂、憎水密闭的混凝土表面处理、涂层等技术的发展,当钢筋周围混凝土中Cl-含量达到临界值时,钢筋腐蚀发展阶段仍可以通过有效的技术措施大幅延长。例如使用高性能混凝土可使该阶段延长至15~30 a[6];在混凝土表面涂刷渗透型阻锈剂能使表面憎水,降低Cl-的渗透,还能明显提高钢筋的腐蚀电位并降低已锈蚀钢筋的腐蚀速率。因此对钢筋腐蚀发展阶段的控制、延长与预测已逐渐成为研究海洋环境中钢筋混凝土构筑物服役寿命的重要组成部分。同时,混凝土保护层开裂的预测结果也是评估构筑物服役寿命的重要指标。钢筋与混凝土的黏结力在钢筋锈蚀初期增大;后期随着保护层的开裂,黏结力逐渐降低,这意味着保护层开裂时间的预测结果对黏结力与钢筋腐蚀程度关系、维修加固决策、耐久性结构设计意义重大。
基于此,笔者定义海洋环境钢筋混凝土构筑物的全寿命T为钢筋腐蚀诱导阶段t0和腐蚀发展阶段t1这两个时段之和,并通过预测模型对t0和t1进行计算。该全寿命预测模型的主要意义有:①在新建海洋环境构筑物之前,基于构筑物所处的具体环境特点及服役寿命要求,通过全寿命预测对各可控参数进行优选;②计算和监控构筑物服役期间的Cl-渗入含量,评估现有混凝土构筑物的剩余使用寿命,对构筑物的安全性、耐久性进行预警监控;③辅助决策构筑物修复加固的时机(t0、t1)、技术措施(涂层封闭、喷涂迁移渗透型阻锈剂、破除修补加固)等;④为构筑物经济寿命周期的预测提供重要的时效参数。
1. 腐蚀诱导阶段的预测
1.1 氯离子扩散基本模型
Cl-从海洋环境通过孔隙、微裂缝向混凝土内部传输的过程非常复杂,主要通过毛细管作用、渗透、扩散、电化学迁移等几种组合方式完成,另外还受Cl-与混凝土间化学结合、物理黏结、吸附等作用影响。扩散是最主要的传输方式。大量试验结果表明,Cl-沿保护层的含量分布是线性扩散方程,一般用Fick第二扩散定律描述:假定混凝土中孔隙是均匀分布的;Cl-的扩散是一维的,浓度梯度仅沿着暴露表面向钢筋方向变化且不与混凝土结合[7-9],见式(1)。

(1) 式中:C为距混凝土表面x处Cl-的质量分数(Cl-与水泥或混凝土质量比);t为构筑物暴露于海洋环境的时间;x为距表面的距离;D为混凝土中Cl-扩散系数。
当构筑物经长时间使用,表面Cl-含量基本稳定,且构筑物整体对于暴露表面为半无限介质,任何时刻无限远处的Cl-含量为初始含量时,相应边界、初始条件可以写为:
边界条件:
 ;
;
初始条件:C(x,0)=C0;将式(1)解为基本扩散模型,见式(2)。

(2) 式中:C(x,t)为t时刻x深度处的Cl-质量分数;C0为混凝土内的初始Cl-质量分数,由试验测定;Cs为混凝土暴露表面Cl-质量分数,取值为海水中Cl-质量分数1.938%;erf(z)为高斯误差函数,
 。
。
1.2 扩散模型的修正
1.2.1 D的时间依赖性修正
式(2)描述的是一种稳态扩散过程。而混凝土的水化需要很长时间才能完成。混凝土成熟度对Cl-扩散影响很大,水化越充分,成熟度越高,内部越密实,抗Cl-渗透的能力就越强。因此Cl-扩散系数是一个时间依赖性函数。MANGAT等[10]在Cl-扩散中考虑Cl-扩散系数与时间的关系,引入有效扩散系数Dt来表示混凝土从开始暴露到检测时的扩散系数均值,且认为二者存在如式(3)所示关系:

(3) 式中:D0为tn时刻混凝土中Cl-扩散系数,按NT BUILD443规定的检测方法最接近实际Cl-扩散;tn为水化龄期;m为Cl-扩散的时间依赖性常数,由试验获得,MANGAT等[10]测得龄期180 d混凝土的m为0.52;THOMAS等[7]测得龄期8 a的粉煤灰混凝土的m为0.7;鉴于高性能混凝土更长的使用寿命,m取0.64[5]。
水化基本完成后,内部微结构基本不再变化,此时Cl-扩散系数趋于恒定。为防止Dt无限降低,式(3)仅适用前30 a;而30 a后,Dt成为恒值。
1.2.2 氯离子结合能力修正
混凝土对Cl-结合主要通过:Cl-被C3AH6化学结合成C3AH6·CaCl2·12H2O;水泥水化时进入CSH凝胶结构;CSH凝胶对Cl-的固溶效应;混凝土内部孔隙与毛细孔表面的物理吸附作用。混凝土与Cl-结合对构筑物寿命影响显著[11]。PREZZI等[8]计算混凝土中Cl-扩散系数时,考虑了混凝土对Cl-的结合,但扩散方程中未引入该参数。
一般认为只有自由Cl-才能导致钢筋锈蚀,钢筋锈蚀的临界值应以自由Cl-含量为标准。而式(2)计算结果为混凝土中自由Cl-质量分数Cf和结合Cl-质量分数Cb组成的Cl-总质量分数C(x,t),即:

(4) 混凝土中Cl-结合能R为:

(5) 式中:普通混凝土的R为2~4,高性能混凝土的R为3~15[5]。
1.2.3 氯离子扩散劣化效应修正
混凝土尤其是高性能混凝土,内部产生微裂纹等缺陷后会加速Cl-的扩散,混凝土干缩和自收缩较大,导致混凝土的微裂缝增加,渗透性增强。材料劣化对Cl-扩散的影响可用等效扩散系数De表示,见式(6)。

(6) 式中:K为混凝土中Cl-扩散性劣化效应系数,普通混凝土的K为1~14,高性能混凝土的K≥6[5]。
1.3 修正后Cl-扩散模型
在Fick定律基础上,综合考虑Cl-扩散的时间依赖性、混凝土与Cl-结合、结构缺陷导致的材料劣化对Cl-扩散的影响,得到修正后的Cl-扩散方程,见式(7)。

(7) 在与1.1节同样的初始、边界条件下得到混凝土中Cl-扩散理论模型,见式(8)。

(8) 由式(8)计算当混凝土保护层深度x处的自由Cl-质量分数C(x,t)达到引起钢筋开始锈蚀的临界Cl-质量分数Ccr时所经历的时间即为腐蚀诱导阶段t0。《混凝土中金属腐蚀防护指南》中,临界Cl-质量分数Ccr的取值为0.25%~0.30%(Cl-与水泥的质量比);我国海港工程调查及华南海港工程暴露试验结果表明,浪溅区混凝土Ccr为0.059%~0.107%(Cl-与混凝土质量比)。综合考虑各种因素并考虑一定的安全储备,海港工程浪溅区用于寿命预测的Ccr取0.05%较为合理[12],即:

(9) 将式(8)变形为式(9),然后经反函数推算,取保护层厚度为C,可得腐蚀诱导时间t0,见式(10)。

(10) 式中:erf(z)是
 反误差函数。将各参数的取值汇总于表1[12]。
Table 1. Parameters and their common values for predicting corrosion initiation time
反误差函数。将各参数的取值汇总于表1[12]。
Table 1. Parameters and their common values for predicting corrosion initiation time参数t0 C(x,t) C0 Cs Ccr D0 t0 m R K x 常用取值 混凝土质量的0.012 5% 海水中的Cl-质量分数1.938% 混凝土质量的0.05% NT BUILD443方法测定的28 d Cl-扩散系数 28 d即0.077 a 0.64 3~15 6~14 混凝土保护层厚度C — 2. 腐蚀发展阶段的模型预测
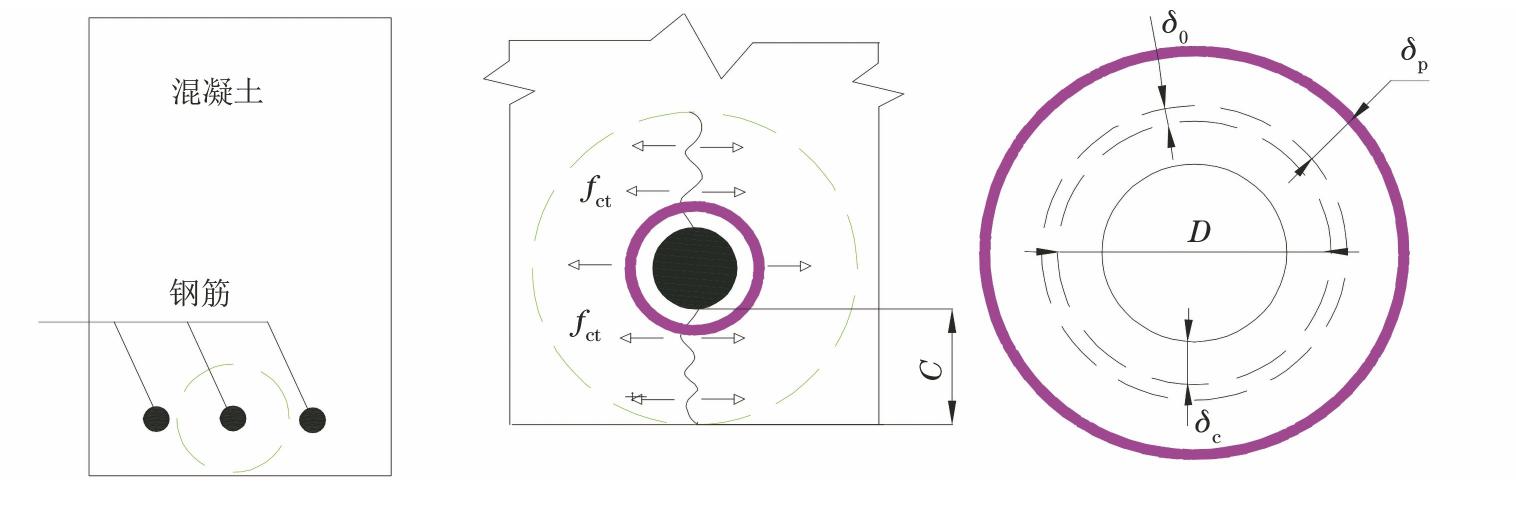
关于钢筋腐蚀造成保护层开裂的机理及预测,国内外进行了大量研究[13-20]。BAZANT[13]根据钢筋锈蚀理论,获得保护层开裂时的临界锈胀力。LIU等[14]应用弹性理论建立了考虑钢筋与混凝土界面间隙多孔区的锈胀开裂模型。CADY等[15]基于试验提出氯盐下钢筋混凝土结构剩余使用寿命预测模型。金伟良等[16]根据弹性力学理论建立了预测钢筋锈胀应力的理论模型。笔者结合已有研究成果,考虑钢筋与混凝土界面间隙多孔区对钢筋初期锈胀的缓冲作用,基于弹性与断裂力学[17-19],计算当混凝土保护层最薄弱区达到其极限拉应力时的钢筋径向锈胀应力,然后利用法拉第定律预测从钢筋开始锈蚀到达到该锈胀应力所需的时间,该段时间即为发展阶段t1。
2.1 基本假定
钢筋与混凝土界面间隙多孔,存在泌水区,腐蚀产物填充该区域后,形成的锈胀应力才能作用于保护层薄弱区;钢筋的弹性模量大于混凝土一个数量级,忽略钢筋的变形;腐蚀产物与腐蚀应力沿钢筋均匀分布;开裂总在保护层的最薄弱区发生;钢筋与开裂区混凝土保护层形成环状圆柱筒体。这些假定已被广泛用于计算钢筋腐蚀膨胀体积、锈胀应力与混凝土极限抗拉强度[13-14,21-25]。
为便于查阅,将各参数按大致出现顺序汇总于表2。
表 2 腐蚀发展阶段的预测参数及其取值、单位Table 2. Parameters, common values, units for predicting corrosion propagation time参数 参数意义(取值或单位) 参数 参数意义(取值或单位) a 环状筒体内径,cm δr 腐蚀产物总厚度,μm b 环状筒体外径,cm ρr 腐蚀产物密度,g·cm-3 ν 混凝土筒体泊松比,0.18 ρs 钢筋密度,g·cm-3 Eef 筒体的有效弹性模量,用式  计算,其中Ec、φc分别为混凝土的弹性模量、徐变系数(2.35)
计算,其中Ec、φc分别为混凝土的弹性模量、徐变系数(2.35)Pcor 径向锈胀应力 Ec 混凝土弹性模量 δP 混凝土径向变形 φc 徐变系数,2.35 Mst 腐蚀前钢筋质量,g δ0 钢筋-混凝土界面层厚度,10~20 μm mγ 钢筋腐蚀率,% D 未锈蚀前钢筋直径,cm Pcr 开裂时径向锈胀应力 D1 D+2δ0 fct 混凝土极限抗拉应力 C 最薄保护层厚度,cm I 腐蚀电流,A τ 与C、D1有关的参数 MFe 铁的摩尔质量,56 g·mol-1 Mc 发生锈蚀的钢筋质量,g T 腐蚀时间(全寿命), a Mr 腐蚀产物的质量,g F 法拉第常数,96 500 C·mol-1 μ Mc/Mr,0.523~0.622 z 铁变成二价铁而失去的电子数,2 V 钢筋锈蚀的膨胀体积 i 腐蚀电流密度,μA·cm-2 δc 钢筋被腐蚀掉的厚度,μm t1 腐蚀发展阶段,a 2.2 锈胀应力的计算
在由钢筋与保护层形成的二环圆柱筒体中,假设钢筋锈蚀使混凝土保护层产生径向锈胀应力Pcor时,混凝土保护层径向变形量为δP,二者关系见式(11):

(11) k为筒体径向应力与内外径的关系,表示为:

(12) 推断钢筋与保护层形成的二环筒体k值,并考虑钢筋与混凝土界面间隙多孔区的缓冲效应时:

(13) 设
 将(11)、(13)合并:
将(11)、(13)合并:

(14) 钢筋锈蚀时发生腐蚀反应的钢筋质量为Mc,腐蚀厚度δc;形成腐蚀产物的质量为Mr,腐蚀产物总厚度δr,单位长度钢筋发生锈蚀的体积膨胀V为:

(15) 钢筋的总锈蚀厚度δr,间隙层厚度δ0,钢筋被腐蚀的厚度δc与混凝土径向变形δP之间的关系见式(16):

(16) 将(16)代入(15),化简得:

(17) 钢筋腐蚀生成单位长度腐蚀产物的质量Mr与生成该锈蚀产物的钢筋原质量Mc的关系为:

(18) μ的取值与腐蚀产物的种类及生成量有关,一般为0.523~0.622[13-14]。
由式(11),(13),(15),(18)得出钢筋锈蚀对保护层产生的径向锈胀应力Pcor为:

(19) 腐蚀产物的密度ρr与锈蚀前钢筋密度ρs[14]的关系为:

(20) 钢筋mγ:

(21) 式中:Mst为腐蚀前单位长度钢筋的质量。

(22) 将式(20)、(21)、(22)代入式(19),并取μ为0.622,经简化得出径向锈胀应力与钢筋腐蚀率mγ的关系:

(23) 2.3 保护层断裂模型
假设梁截面混凝土保护层与钢筋形成的环形筒体如图2所示,钢筋锈蚀后,锈蚀产物填充满钢筋与混凝土的多孔界面层后,锈胀应力作用于环状筒壁并逐渐增大,当锈胀应力超过筒体材料的极限抗拉应力fct时,保护层沿薄弱区开裂。此时径向锈胀应力Pcr与极限抗拉应力fct静力平衡:

(24) 由于钢筋腐蚀层厚度远小于钢筋直径和保护层厚度,上式简化得:

(25) 将式(25)代入式(23)得钢筋腐蚀率mγ与保护层极限拉应力fct的关系为:

(26) 2.4 发展阶段预测
国内外学者[26-30]用法拉第定律来预测从腐蚀开始到保护层胀裂的时间t1,通过监测钢筋的腐蚀电流来预测钢筋的锈蚀量Mc,进而建立其与极限径向锈胀应力Pcr的关系。
钢筋腐蚀量Mc与腐蚀电流I的关系为:

(27) 设钢筋的表面积为As,腐蚀电流密度为i;将式(21)、(22)代入(27)化简得:

(28) 将钢筋密度7.85 g/cm3代入上式,并进行单位换算得:

(29) 将(29)式代入(26)得钢筋开始腐蚀至混凝土保护层开裂时间t1:

(30) 3. 全寿命预测
将腐蚀诱导阶段t0和腐蚀发展阶段t1这两个时段相加即为海洋环境钢筋混凝土构筑物的全寿命T:

(31) 因此影响全寿命的主要参数有:D0, Cs,C0, CCR, C, D, E, fct。
目前,国内外对混凝土构筑物的寿命预测方法大致分为五类,即经验预测法、随机变量法、数值模型法、加速试验法和比较法[31]。
经验预测法通过对大量现场实测数据以及长期可靠的经验累积,对混凝土构筑物的寿命进行半定量化预测,如采用回归分析法,此过程是经验知识积累与直观推测的结合与归纳。但采用此方法的前提是结构的设计寿命短、侵蚀破坏行为小,且服役环境稳定,如此方可达到结构本身预期中的设计使用寿命。
基于影响构筑物寿命的各因素不易归纳或很难进行定量描述,如混凝土保护层厚度、孔隙率等都是随机过程,采用概率方法对构筑物的剩余使用寿命进行预测是比较合理的,但实施过程中因素的变化较为复杂。
数值模型法可以较为合理地预测混凝土构筑物的使用寿命,在模型构建合理、材料与环境参数选取准确的前提下,预测结果可靠性较高。但此方法通常只能针对特定的建筑,一旦改变任一参数,结果也将相应发生改变,因此适用范围较为狭窄。
加速试验法基于室内试验,分析影响混凝土构筑物耐久性参数变化的不同破坏因素,构建劣化方程,找出试件的破坏时间阈值,以此确定混凝土的使用寿命。但该方法无法完全模拟实际环境中的所有因素,其结果可能存在一定误差。
对比预测法通过假定已知环境中混凝土构筑物的实际耐久性与工作年限,反映相似环境中相似材料混凝土构筑物的使用寿命。但是,不同构筑物具有其独特的材料使用量、施工质量、荷载状况、服役环境,且随着混凝土材料的不断改进,其性能与之前大不相同。因此该方法采用率较低,有一定的局限性。
4. 结论
混凝土技术的发展使得钢筋周围混凝土中Cl-到达临界含量后,钢筋腐蚀发展阶段t1仍可以通过有效的技术措施大幅延长。将海洋环境钢筋混凝土构筑物的全寿命T定义为腐蚀诱导阶段t0和腐蚀发展阶段t1两个时段之和,并分别对t0和t1进行模型预测计算。
腐蚀诱导阶段t0:在Fick第二扩散定律的基础上,考虑混凝土与Cl-结合能力、Cl-扩散系数的时间依赖性以及材料内部结构缺陷对Cl-扩散性能劣化的影响,建立多种因素影响下的混凝土Cl-扩散理论模型。然后对该模型经过严密的理论推导,计算钢筋周围混凝土中Cl-含量达到使钢筋腐蚀所需的时间t0。
腐蚀发展阶段t1:基于弹性与断裂力学,考虑钢筋与混凝土界面间隙多孔区对钢筋初期锈胀的缓冲作用,计算钢筋开始腐蚀至混凝土保护层开裂所需的时间t1。
-
Table 1 Parameters and their common values for predicting corrosion initiation time
参数t0 C(x,t) C0 Cs Ccr D0 t0 m R K x 常用取值 混凝土质量的0.012 5% 海水中的Cl-质量分数1.938% 混凝土质量的0.05% NT BUILD443方法测定的28 d Cl-扩散系数 28 d即0.077 a 0.64 3~15 6~14 混凝土保护层厚度C — 表 2 腐蚀发展阶段的预测参数及其取值、单位
Table 2 Parameters, common values, units for predicting corrosion propagation time
参数 参数意义(取值或单位) 参数 参数意义(取值或单位) a 环状筒体内径,cm δr 腐蚀产物总厚度,μm b 环状筒体外径,cm ρr 腐蚀产物密度,g·cm-3 ν 混凝土筒体泊松比,0.18 ρs 钢筋密度,g·cm-3 Eef 筒体的有效弹性模量,用式  计算,其中Ec、φc分别为混凝土的弹性模量、徐变系数(2.35)
计算,其中Ec、φc分别为混凝土的弹性模量、徐变系数(2.35)Pcor 径向锈胀应力 Ec 混凝土弹性模量 δP 混凝土径向变形 φc 徐变系数,2.35 Mst 腐蚀前钢筋质量,g δ0 钢筋-混凝土界面层厚度,10~20 μm mγ 钢筋腐蚀率,% D 未锈蚀前钢筋直径,cm Pcr 开裂时径向锈胀应力 D1 D+2δ0 fct 混凝土极限抗拉应力 C 最薄保护层厚度,cm I 腐蚀电流,A τ 与C、D1有关的参数 MFe 铁的摩尔质量,56 g·mol-1 Mc 发生锈蚀的钢筋质量,g T 腐蚀时间(全寿命), a Mr 腐蚀产物的质量,g F 法拉第常数,96 500 C·mol-1 μ Mc/Mr,0.523~0.622 z 铁变成二价铁而失去的电子数,2 V 钢筋锈蚀的膨胀体积 i 腐蚀电流密度,μA·cm-2 δc 钢筋被腐蚀掉的厚度,μm t1 腐蚀发展阶段,a -
[1] CLIFTON J R. Predicting the service life of concrete[J]. ACI Material Journal, 1993, 90(6): 611-17. [2] AMEY S L, JOHNSON D A, MILTENBERGER M A. Prediction the service life of concrete marine structures: an environmental methodology[J]. ACI Structural Journal, 1998, 95(2): 205-14. [3] MAAGE M, HELLAND S, CARLSEN J E. Service life prediction of existing concrete structures exposed to marine environment[J]. ACI Material Journal, 1996, 93(6): 602-08. [4] LIANG M T, WANG K L LIANG C H. Service life prediction of reinforced concrete structures[J]. Cement and Concrete Research, 1999, 29: 1411-18. [5] 余红发, 孙伟. 混凝土使用寿命预测方法的研究I-理论模型[J]. 硅酸盐学报, 2002, 30(6): 686-89. YU H F, SUN W. Study on prediction of concrete of concrete service life I-theoretical model[J]. Journal of the Chinese ceramic society, 2002, 30(6): 686-89.
[6] RICHARD E W. Service life model for concrete structure in chloride environment[J]. ACI Materials Journal, 1998, 95(4). [7] THOMAS M D A, BAMFORTH P B. Modeling chloride diffusion in concrete-Effect of fly ash slag[J]. Cement and Concrete Research, 1999, 29(4): 487-95. [8] PREZZI M, GEYSKENS P, MONTEIRO P J M. Reliability approach to service life prediction of concrete exposed to marine environment[J]. ACI Materials Journal, 1996, 93(6): 544-552. [9] MANGAT P S, MOLLOY B T. Prediction of long term chloride concentration in concrete[J]. Materials and Structures, 1994, 27(6): 338-346. [10] MANGAT P S, LIMBACHIYA M C. Effect of initial curing on chloride diffusion in concrete repair materials[J]. Cement and Concrete Research, 1999, 29(9): 1475-1485. [11] 谢友均, 陈书苹, 龙广成. 改善水泥浆体结合氯离子性能的试验研究[J]. 铁道科学与工程学报, 2007, 4(2): 1-5. XIE Y J, CHEN S P, LONG G C. Experimental study on improvement of chloride ion binding of cement paste[J]. Journal of Railway Science and Engineering, 2007, 4(2): 1-5.
[12] 王信刚跨江海隧道功能梯度混凝土管片的研究与应用武汉武汉理工大学2007王信刚. 跨江海隧道功能梯度混凝土管片的研究与应用[D]. 武汉: 武汉理工大学, 2007. WANG X GResearch and application of functionally graded concrete segment for river-sea tunnelWuhanWuhan University of Technology2007WANG X G. Research and application of functionally graded concrete segment for river-sea tunnel[D]. Wuhan: Wuhan University of Technology, 2007.
[13] BAZANT Z P. Physical model for steel corrosion in concrete sea structures-theory[J]. Journal of the Structural Division, 1979, 105(6): 1137-1153. [14] LIU Y, WEYERS R E. Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures[J]. ACI Materials Journal, 1998, 95(6): 675-81. [15] CADY P D, WEYERS R E. Chloride penetration and the deterioration of concrete bridge decks[J]. Cement, Concrete, and Aggregates, 1983, 5(2): 81-87. [16] 金伟良, 赵羽习, 鄢飞. 钢筋混凝土构件的均匀钢筋锈胀力的机理研究[J]. 水利学报, 2001, 32(7): 57-62. JIN W L, ZHAO Y X, YAN F. The mechanism of corroded expansion force of reinforced concrete members[J]. Journal of Hydraulic Engineering, 2001, 32(7): 57-62.
[17] MOLINA F J, ALONSO C, ANDRADE C. Cover cracking as a function of rebar corrosion: part 2—numerical model[J]. Materials and Structures, 1993, 26(9): 532-548. [18] HANSEN E J, SAOUMA V E. Numerical simulation of reinforced concrete deterioration: part II steel corrosion and concrete cracking[J]. ACI Materials Journal 1999; 96(3): 331-8. [19] PANTAZOPOULOU S J, PAPOULIA K D. Modeling cover-cracking due to reinforcement corrosion in RC structures[J]. Journal of Engineering Mechanics, 2001, 127(4): 342-351. [20] EL MAADDAWY T, SOUDKI K. A model for prediction of time from corrosion initiation to corrosion cracking[J]. Cement and Concrete Composites, 2007, 29(3): 168-175. [21] CHARRON J P, PLIZZARI G, MOBASHER B. fib Bulletin 79. Fibre-reinforced concrete: From design to structural applications[M]. [S.l.]: The International Federation for Structural Concrete, 2017. [22] CAPOZUCCA R. Damage to reinforced concrete due to reinforcement corrosion[J]. Construction and Building Materials, 1995, 9(5): 295-303. [23] OHTSU M, YOSIMURA S. Analysis of crack propagation and crackinitiation due to corrosion of reinforcement[J]. Construction and Building Materials, 1997, 11(7/8): 437-442. [24] JIMENEZ R, WHITE RN, GERGELY P. Bond and dowel capacities of reinforced concrete[J]. ACI J 1979; 76(4): 73-92. [25] TEPFERS R. Cracking of concrete cover along anchored deformed reinforcing bars[J]. Magazine of Concrete Research, 1979, 31(106): 3-12. [26] ANDRADE C, ALONSO C, MOLINA FJ. Cover cracking as a function of bar corrosion: part I-experimental test[J]. Material Structure, 1993; 26: 453-64. [27] CABRERA J G. Deterioration of concrete due to reinforcement steel corrosion[J]. Cement and Concrete Composites, 1996; 18: 47-59. [28] MANGAT P S, ELGARF M S. Bond characteristics of corroding reinforcement in concrete beams[J]. Mater Struct, 1999; 32: 89-97. [29] YOON S, WANG K, WEISS W J, et al. Interaction between loading, corrosion, and serviceability of reinforced concrete[J]. ACI Mater J 2000; 97(6): 637-44. [30] EL MAADDAWY T, SOUDKI K. Effectiveness of impressed current technique to simulate corrosion of steel reinforcement in concrete[J]. ASCE J Material Civil Engineering 2003; 15(1): 41-7. [31] MARCHAND J, SAMSON E. Predicting the service-life of concrete structures-Limitations of simplified models[J]. Cement and concrete composites, 2009, 31(8): 515-521.



 下载:
下载: