High Temperature Fatigue Deformation Behavior and Life Prediction of 316L Stainless Steel under Different Control Modes
-
摘要:
在550 ℃下对核电用316L不锈钢进行应变控制（应变幅在0.3%~1.2%）、应力控制（应力幅在230~300 MPa）低周疲劳试验和应变控制蠕变疲劳试验（3种波形,拉伸保载60,180,600 s,压缩保载60,180 s,拉压对称保载180 s）,通过疲劳寿命、循环响应特征和应力-应变滞回曲线分析了不同控制模式下试验钢的疲劳变形行为；构建疲劳寿命预测模型,评估了Manson-Coffin-Basquin模型、SWT模型和能量法模型对不同控制模式下试验钢疲劳寿命的预测能力。结果表明：在不同控制模式的疲劳循环载荷下,316L不锈钢的循环应力响应均包括循环硬化、循环软化和失效断裂3个阶段；在低周疲劳试验中,疲劳寿命随应变幅或应力幅的增大而缩短；在蠕变疲劳试验中,疲劳寿命随拉伸保载时间的延长而缩短,随压缩保载时间的延长而增大,这与动态应变时效和蠕变对疲劳损伤的综合作用有关；在相同保载时间下,压缩保载下的疲劳寿命比拉伸保载下的短,这与不同加载方向引起的氧化层致裂机制有关。能量法模型对316L不锈钢在不同控制模式下的疲劳寿命预测精度最高,预测精度在1.5倍误差带以内,Manson-Coffin-Basquin模型的预测精度最低。
Abstract:Strain controlled (strain amplitude of 0.3%-1.2%) and stress controlled (stress amplitude of 230-300 MPa) low cycle fatigue tests, and strain controlled creep fatigue tests (three waves including tensile holding for 60, 180, 600 s, compressive holding for 60, 180 s and tensile and compressive symmetric holding for 180 s) at 550 ℃ were conducted on 316L stainless steel for nuclear power. The fatigue deformation behaviour of the test steel under different control modes was analyzed through fatigue life, cyclic response characteristics and stress-strain hysteresis curves. The fatigue life prediction models including Manson-Coffin-Basquin model, SWT model, and energy method model were constructed and the predictive ability of these models for fatigue life of the test steel under different control modes was evaluated. The results show that the cyclic stress response of 316L stainless steel included cyclic hardening, cyclic softening and failing fracture stages under fatigue cyclic load of different control modes. In the low cycle fatigue test, the fatigue life decreased with the increase of strain or stress amplitude. In the creep fatigue test, the fatigue life decreased with the extension of tensile holding time and increased with the extension of compressive holding time, which was related to the comprehensive effect of dynamic strain aging and creep on fatigue damage. Under the same holding time, the fatigue life under compressive holding was shorter than that under tensile holding, which was related to the cracking mechanism of oxide layer caused by different loading directions. The energy method model had the highest accuracy in predicting the fatigue life of 316L stainless steel under different control modes, with prediction accuracy within 1.5 times the error band, and the Manson-Coffin-Basquin model had the lowest prediction accuracy.
-
0. 引言
在石油、化工和核电等行业中,低周疲劳、蠕变疲劳是导致高温装备过早失效的主要原因[1]。高温装备在启动和停车过程中会出现温度瞬变,使材料承受由热应力产生的低周疲劳载荷；而在稳定运行期间,材料则会承受高温蠕变载荷,引起蠕变损伤[2]。因此,在设计及评估上述高温装备时不仅需要考虑设备启动和停车过程造成的低周疲劳损伤,同时还需要考虑设备在整个服役周期内承受的蠕变-疲劳交互损伤。
在低周疲劳行为的研究中,根据控制方式的不同可将低周疲劳试验分为应变控制和应力控制两种模式,分别通过控制应变幅或应力幅大小来研究材料疲劳寿命的演化规律。ZHONG等[3]对国产核电主管道材料316LN不锈钢进行疲劳试验,发现峰值应力与应变幅正相关,在大应变幅下,材料出现先循环硬化后循环软化最终失效的现象,而在小应变幅下未出现明显的循环硬化/软化特征。YUAN等[4]对316LN不锈钢进行对称应力控制与应变控制的疲劳试验后发现,2种控制方式下316LN不锈钢的循环响应规律相似,即大幅值下表现出先硬化后软化的特征,而小幅值下还会引入额外的二次硬化现象。在蠕变疲劳性能的研究方面,WALKER等[5]最早通过在峰值应变处进行保载来研究材料的蠕变疲劳性能,目前这种方法被大部分学者所采用。WANG等[6]在600 ℃下对P92钢的蠕变疲劳行为进行研究,发现引入保载后,峰值应力降低,寿命缩短,软化现象严重且随保载时间的延长而趋于饱和。HORMOZI等[7]在高温下对316钢进行不同应变幅的蠕变疲劳试验,发现应变幅越大,流动应力和塑性应变越大,滞回曲线包围的面积也越大。此外,引入保载会导致应力松弛,且随着温度的升高,该现象更加明显[8]。综上发现,已有研究大都局限于应变控制或应力控制模式的单一疲劳载荷,鲜有系统研究多种控制模式下疲劳与蠕变疲劳损伤区别的报道。
在高温疲劳寿命预测方面,国内外学者提出了多种预测模型,包括基于Manson-Coffin方程、基于区分方法和基于线性损伤累积准则的三大类模型[9]。YUAN等[4]采用Basquin模型和Manson-Coffin模型成功预测了316LN不锈钢在室温和350 ℃下不同应变/应力幅的低周疲劳寿命；SMITH等[10]在Manson-Coffin-Basquin模型的基础上,纳入平均应力对316不锈钢寿命的影响,提出了Smith-Watson-Topper（SWT）模型。然而,目前大多数疲劳寿命预测方法只针对单一控制模式的循环载荷,而相关模型在不同控制模式疲劳载荷下的适用性尚未有统一结论。
316L不锈钢是核电站液态金属反应堆容器、回路管道等关键部件的常用材料,研究其在实际核电工况不同控制模式下的高温疲劳变形特性、损伤机理及寿命预测,对提高在役装备的安全可靠性具有重要的价值。基于此,作者在550 ℃下对316L不锈钢进行一系列的应变控制低周疲劳、应力控制低周疲劳和应变控制蠕变疲劳试验,系统研究不同控制模式下316L不锈钢的循环变形行为、损伤演化和寿命规律,并采用常用的寿命预测模型来预测不同循环载荷下的疲劳寿命,分析其预测能力,筛选出具有广泛载荷适应能力的模型。
1. 试样制备与试验方法
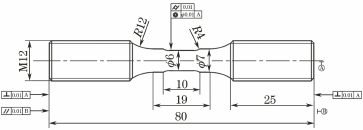
试验材料选用外径为220 mm、壁厚为25 mm的316L不锈钢管,由浙江久立特材科技有限公司提供,其热处理工艺为1 040 ℃固溶水淬,化学成分及拉伸性能分别如表1和表2所示。试验钢的显微组织为如图1所示的典型奥氏体组织。在GB/T 15248—2008标准疲劳试样的基础上进行改进,改进的疲劳试样标距段长度为10 mm,直径为6 mm,具体尺寸如图2所示。对试样标距段进行精抛处理至表面粗糙度Ra低于0.2μm,以消除表面缺陷对试样疲劳性能的影响。
表 1 316L不锈钢的化学成分Table 1. Chemical composition of 316L stainless steel元素 C Mn P S Si Ni Cr Mo 质量分数/% 0.031 1.11 0.030 0.006 1 0.412 11.78 18.09 2.29 表 2 316L不锈钢的拉伸性能Table 2. Tensile properties of 316L stainless steel温度/℃ 屈服强度/MPa 抗拉强度/MPa 断后伸长率/% 25 289 589 79.8 550 150 378 52.7 采用RPL-100型电子蠕变疲劳试验机进行应变控制低周疲劳（ELCF）试验、应力控制低周疲劳（SLCF）、应变控制蠕变疲劳（CFI）试验,试验温度均为550 ℃。在试验过程中,炉内的温度由上中下3根K型热电偶测试,温度精度控制在±2 ℃。通过力值传感器采集并记录试验载荷,由标距为10 mm的Epsilon引伸计测量试样变形量。按照GB/T 26077—2021进行应变控制低周疲劳试验,应变速率为1×10-3 s-1,加载波形为对称三角波,应变幅分别为0.3%,0.4%,0.6%,0.8%,1.0%,1.2%。按照GB/T 3075—2021进行应力控制低周疲劳试验,应力速率为50 MPa·s-1,加载波形为对称三角波,应力幅分别设定为230,250,270,280,290,300 MPa。按照GB/T 38822—2020进行应变控制蠕变疲劳试验,应变幅为0.4%,应变速率为1×10-3 s-1,加载波形为上梯形波（拉伸保载,记作CFI-T）、下梯形波（压缩保载,记作CFI-C）及对称梯形波（拉压对称保载,记作CFI-TC）,拉伸保载时间分别为60,180,600 s,压缩保载时间分别为60,180 s,拉压对称保载时间为180 s。试样在疲劳试验中的瞬间断裂通常会损坏引伸计,因此需要根据不同的材料及加载方式,采用不同的疲劳失效判定准则（试验判停准则）,在试样达到失效且未产生瞬间断裂前取下引伸计[11-13]。作者基于应变控制与应力控制2种模式的特点,分别将最大峰值应力下降25%、最小应变幅上升60%对应的循环周次定义为失效周次,即疲劳寿命Nf。观察发现,在上述设定的应变幅与应力幅下,应力-应变滞回曲线出现“猪尾状”凸起,这种特征代表了宏观裂纹的产生,因此可判定试样失效。
2. 试验结果与讨论
2.1 循环应力响应
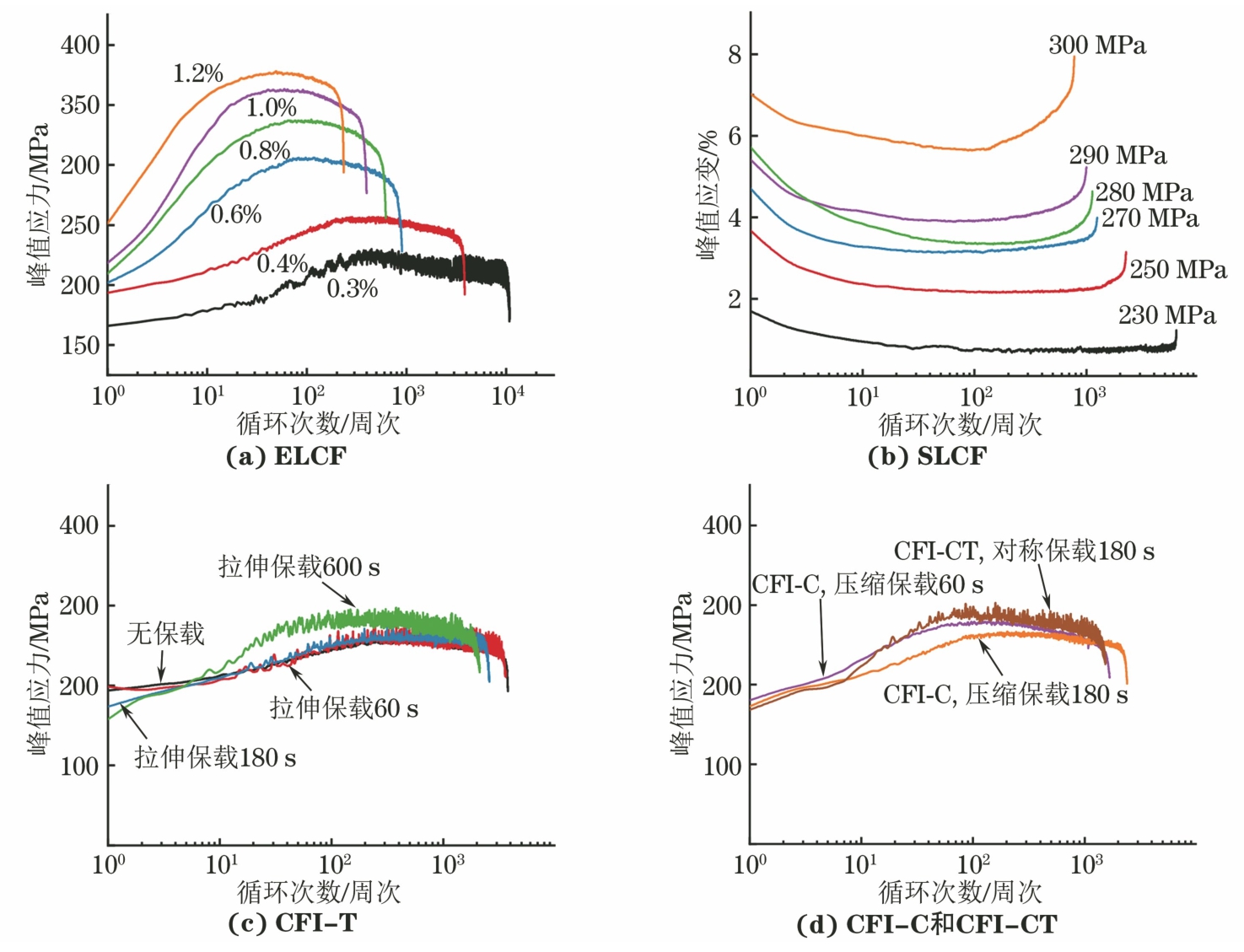
材料的循环应力响应是硬化和软化竞争的结果,受温度、加载速率、应变幅等多因素影响[14]。由图3可见：在不同试验条件下,316L不锈钢均经历先循环硬化再循环软化,最后失效3个阶段；在CFI试验中引入保载后,其峰值应力变化趋势并未发生明显变化。316L不锈钢在循环初期均表现出循环硬化行为,这与位错之间的相互作用、位错上细小沉淀的形成以及位错与溶质原子之间的相互作用有关[14-15]；在循环硬化后表现出了持续循环软化行为,这是因为位错的湮灭率大于生成率,导致位错密度减小,并且先前形成的位错结构随着循环次数的增加发生重排,导致位错平均自由程增加[16-17]。
![]()
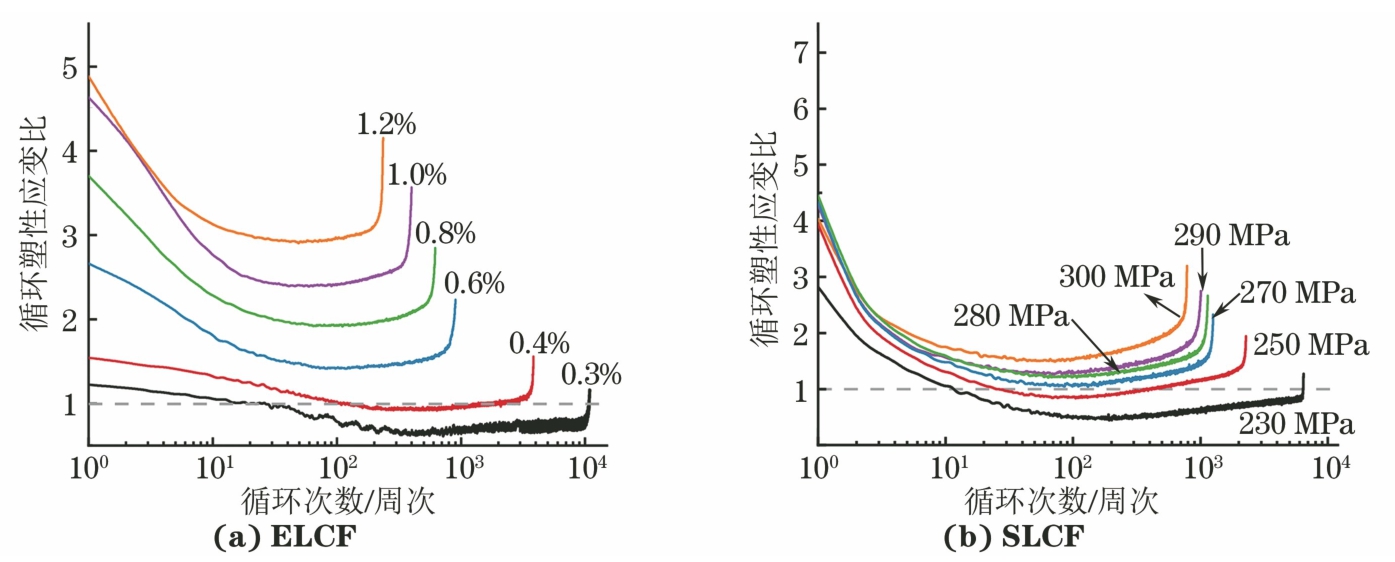
图 3 316L不锈钢在不同试验条件下的峰值应力/应变与循环次数的关系曲线Figure 3. Peak stress/strain vs cycle number curves of 316L stainless steel under different test conditions在疲劳过程中,塑性变形是材料发生内部损伤的关键因素。为进一步研究应变与应力控制2种模式下试验钢的塑性变形行为,作者提出了循环塑性应变比[18-19],其表达式为
(1) 式中：SR为循环塑性应变比；E为弹性模量；Δσa为应力幅；Δεt为总应变幅。
由图4可以看出,当应变幅大于0.4%或应力幅大于250 MPa时,在整个循环周次内,循环塑性应变比均大于1,表明试验钢持续发生塑性变形；而在小应变幅（0.3%）或应力幅（230 MPa）下,循环塑性应变比基本小于1,表明试验钢主要发生弹性变形。
![]()
图 4 316L不锈钢在不同控制模式低周疲劳试验下的循环塑性应变比与循环次数的关系曲线Figure 4. Curves of cyclic plastic strain ratio vs cycle number of 316L stainless steel after low cycle fatigue tests under different control modes2.2 循环应力-应变滞回曲线
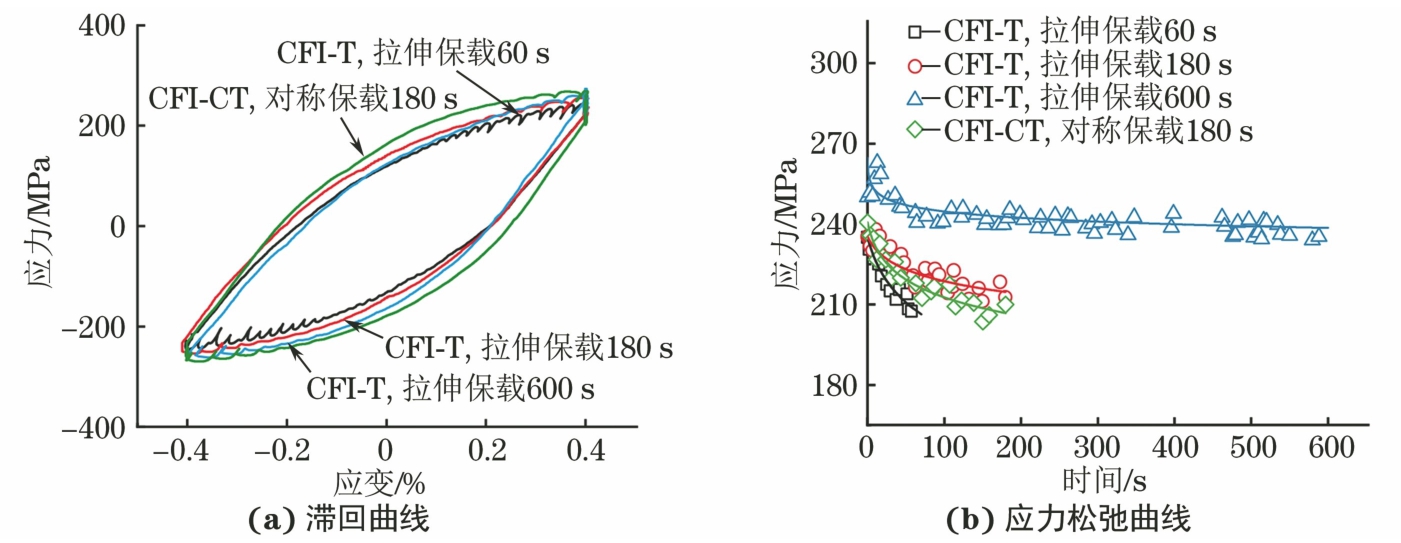
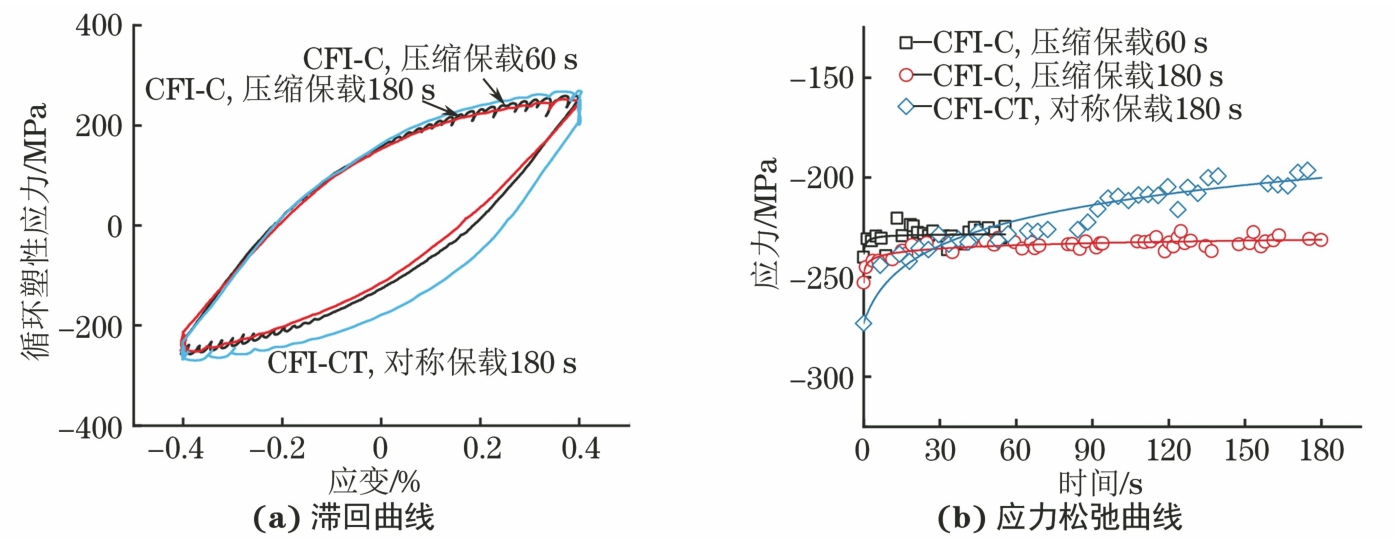
由图5、图6和图7可以看出,在ELCF与CFI试验过程中316L不锈钢的应力-应变滞回曲线在拉伸与压缩加载方向均存在锯齿流动现象,说明试验钢出现了明显动态应变时效（DSA）现象。在试验温度为550 ℃下,316L不锈钢的位错运动并不连续,位错在运动过程中被晶体内部障碍物阻碍,同时溶质原子受位错产生的应力场影响,通过扩散方式向位错偏聚,形成溶质原子气团钉扎可动位错[20-21]；随后在外加应力场作用下,316L不锈钢通过热激活方式克服时效阻碍,可动位错脱钉,导致位错增殖,最终宏观上表现为应力下降或应变突增。316L不锈钢在ELCF试验时的滞回曲线面积随着应变幅的增加而增大,对应的滞回能增大,说明其疲劳损伤增加[22]；SLCF试验下的滞回曲线面积随应力幅的增加表现出与ELCF试验下相似的规律,此外棘轮应变量与应力幅也呈正相关性。CFI试验下的试验钢在达到最大应变后出现应力松弛现象；不同保载方式下,试验钢的应力松弛现象变化不明显,但随着保载时间的延长,应力松弛量逐渐增大。采用Feltham方程[23]进行拟合,表达式为
(2) 式中：α,β为材料参数；t为保载时间；σ0,σr分别为开始保载时的应力以及应力松弛量。
![]()
图 5 316L不锈钢在不同控制模式低周疲劳试验下半寿命时的应力-应变滞回曲线Figure 5. Stress-strain hysteresis curves of 316L stainless steel at half life after low cycle fatigue tests under different control modes![]()
图 6 316L不锈钢在CFI-T和CFI-CT试验下半寿命时的应力-应变滞回曲线和应力松弛曲线Figure 6. Stress-strain hysteresis curves (a) and stress relaxation curves (b) of 316L stainless steel at half life under CFI-T and CFI-CT tests![]()
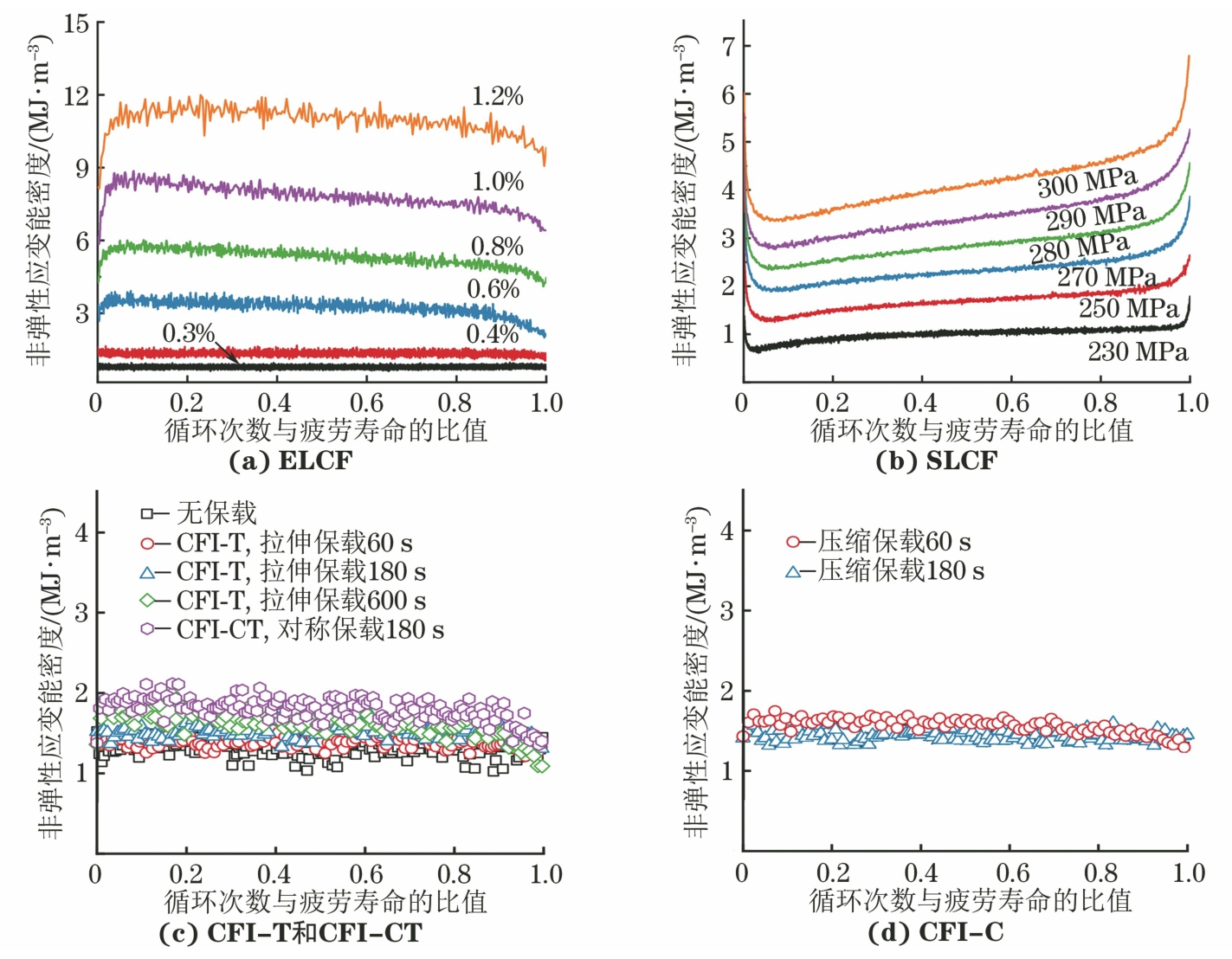
图 7 316L不锈钢在CFI-C和CFI-CT试验下半寿命时的应力-应变滞回曲线和应力松弛曲线Figure 7. Stress-strain hysteresis curves (a) and stress relaxation curves (b) of 316L stainless steel at half life under CFI-C and CFI-CT tests滞回曲线面积（非弹性应变能密度）可以定量地反映材料在疲劳载荷下的损伤程度[22]。由图8可见：在ELCF和SLCF试验中,非弹性应变能密度与应变幅、应力幅呈正相关性,说明在大应变或应力幅下材料的疲劳损伤更显著；在小应变幅（0.3%,0.4%）下,非弹性应变能密度在整个寿命周期内基本不变,而应变幅达到0.6%后非弹性应变能密度先增大后减小；在相同应力幅下,非弹性应变能密度随循环次数的增加呈现先减小再缓慢增大最后迅速增大的趋势。引入拉伸保载后,随着保载时间的延长,非弹性应变能密度增大,说明试验钢的疲劳损伤变严重；然而,引入压缩保载后,随着保载时间的延长,非弹性应变能密度降低,说明试验钢的疲劳损伤变轻。可知,试验钢的疲劳寿命与非弹性应变能密度大小密切相关。
![]()
图 8 不同试验条件下316L不锈钢的非弹性应变能密度变化曲线Figure 8. Inelastic strain energy density curves of 316L stainless steel under different test conditions2.3 疲劳寿命
由表3可知：在应变控制低周疲劳和应力控制低周疲劳试验中,316L不锈钢的疲劳寿命随应变幅或应力幅的增大而缩短；在应变控制蠕变疲劳试验中,其疲劳寿命随拉伸保载时间的延长而缩短,随压缩保载时间的延长而增大,其中拉压对称保载试验的疲劳寿命最短。
表 3 316L不锈钢在不同试验条件下的疲劳寿命试验值Table 3. Fatigue life test values of 316L stainless steel under different test conditions试验 应变幅/% 应力幅/MPa 保载时间/s 疲劳寿命/周次 ELCF 0.3 10 857 0.4 3 835 0.6 903 0.8 619 1.0 398 1.2 235 SLCF 230 6 437 250 2 276 270 1 257 280 1 142 290 1 007 300 784 CFI-T 60 3 624 0.4 180 2 613 600 2 148 CFI-C 0.4 60 1 672 180 2 401 CFI-TC 0.4 180 1 537 在相同应变幅和保载时间下,试验钢在CFI-C试验下的疲劳寿命均比CFI-T短,这归因于不同保载方式的试验钢表面氧化层对起裂机制产生不同影响[24]。在CFI-C试验中,压缩保载阶段生长的氧化层在拉伸阶段破裂,导致试验钢表面重新暴露于高温环境而发生氧化,并在循环加载过程中反复氧化[6]；而在CFI-T试验中,拉伸保载阶段生长的氧化层紧接着承受压缩载荷,不易发生氧化层破裂。因此,拉伸保载引起的损伤小于压缩保载。除了表面氧化层的影响,高温DSA也会导致基体发生不均匀变形,形成严重的局部塑性变形区,从而降低试验钢的疲劳寿命[25]。随着拉伸保载或压缩保载时间的延长,在CFI试验过程中316L不锈钢在半寿命时的应力-应变滞回曲线的锯齿流动现象减弱,说明DSA效应逐渐减弱,对试验钢疲劳寿命的劣化作用减弱[26]；而蠕变造成的疲劳损伤随拉伸保载和压缩保载时间的延长而增大,使得蠕变对疲劳寿命的劣化作用增强[27]。因此,DSA与蠕变二者之间存在综合作用,共同影响着CFI试验下的疲劳寿命。由于拉伸保载时DSA的消退程度较压缩保载弱,拉伸保载时DSA对试验钢疲劳寿命的影响占主导作用,综合损伤随保载时间的延长而增大,因此疲劳损伤增大,疲劳寿命缩短；而压缩保载时蠕变对试验钢疲劳寿命的影响占主导作用,综合损伤随保载时间的延长而减小,因此疲劳损伤减小,疲劳寿命延长。
3. 疲劳寿命预测
3.1 寿命预测模型
在高温条件下,材料塑性应变幅与疲劳寿命的关系可以通过多种表达式进行描述。MANSON和COFFIN[28-29]最早提出的Manson-Coffin模型适用于材料塑性变形主导的低周疲劳试验；而Basquin模型适用于材料弹性变形主导的疲劳试验[30]。由于材料在循环变形过程中会经历弹性和塑性变形,因此结合式（3）和式（4）这2个模型得到式（5）表示的Manson-Coffin-Basquin（MCB）寿命预测模型。
(3) 
(4) 
(5) 式中：Δεin为塑性应变幅；
为疲劳黏性系数；c为疲劳延性指数；
为疲劳强度系数；b为疲劳强度指数；Δεe为弹性应变幅。
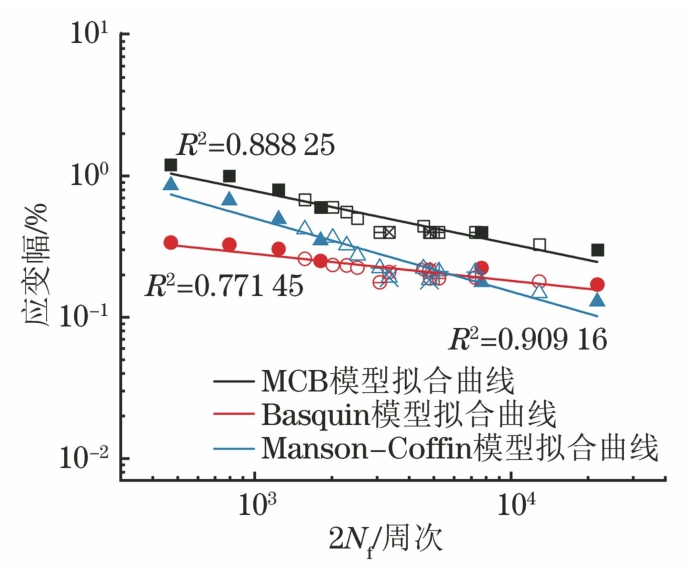
分别采用MCB模型、Basquin模型、Manson-Coffin模型对316L不锈钢在不同控制模式下半寿命时的总应变幅、弹性应变幅、塑性应变幅和疲劳寿命之间的关系进行拟合,得到
为1 292.02 MPa,b为-0.19,
为0.18,c为-0.52,E为123.12 GPa。由图9可见,在双对数坐标下,MCB模型的拟合相关系数R2为0.888 25。
![]()
图 9 316L不锈钢疲劳寿命的MCB模型、Basquin模型、Manson-Coffin模型拟合结果Figure 9. Fitting results of MCB model, Basquin model and Manson-Coffin model for 316L stainless steel fatigue life研究[31]表明,平均应力对材料的疲劳寿命有明显影响。因此,在MCB方程的基础上,SMITH等[10]考虑了平均应力的影响,提出了SWT模型,具体表达式为
(6) 
(7) 式中：σmax为考虑平均应力的疲劳参数；εa为应变幅；σm为平均应力。
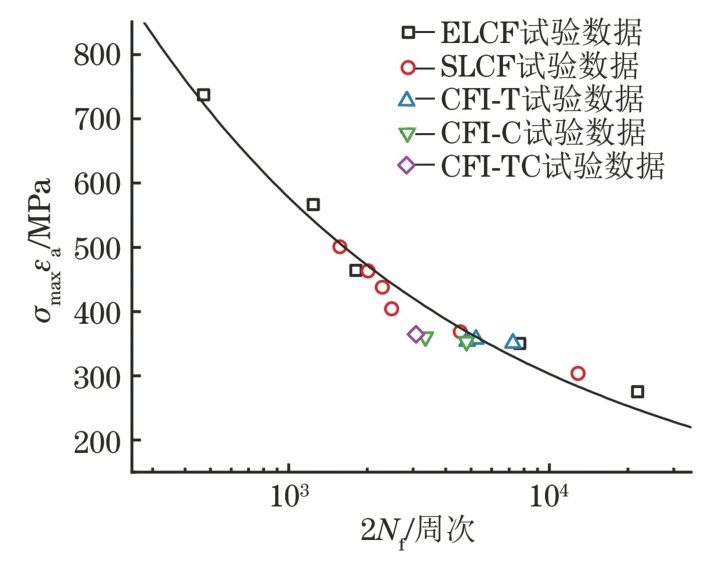
SWT模型可用来描述不同循环载荷下疲劳寿命与σmaxεa之间的关系。316L不锈钢疲劳寿命的SWT模型拟合结果如图10所示。
![]()
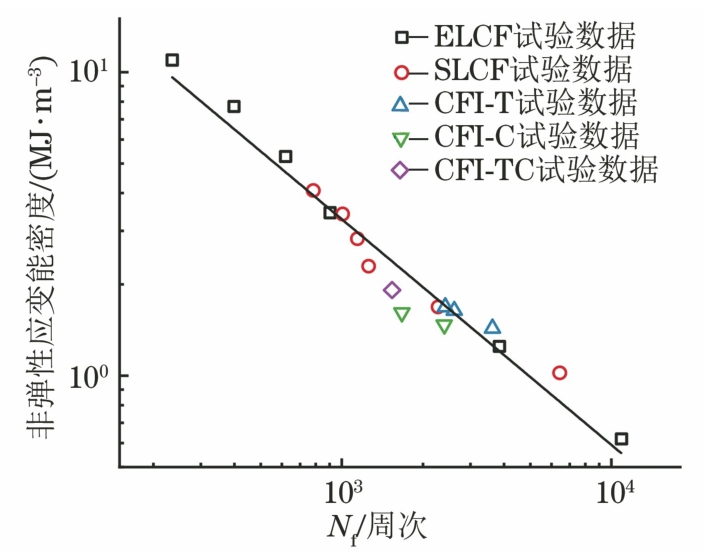
图 10 不同试验条件下316L不锈钢疲劳寿命的SWT模型拟合结果Figure 10. Fitting results of SWT model for 316L stainless steelfatigue life under different conditions材料在高温条件下的疲劳损伤通常由塑性变形引起,这是一个不可恢复的能量耗散过程[32],能量耗散过程能够表征疲劳循环应力和塑性应变对疲劳损伤的影响。每个完整的循环周期都能形成一条滞回曲线,代表着一个周期内的能量耗散过程,其面积等于非弹性应变能密度的大小。疲劳寿命与所消耗能量相关,因此可建立基于非弹性应变能密度的寿命预测模型,即如式（8）所示的能量法（EM）模型[33]。
(8) 式中：ΔWp为半寿命时的非弹性应变能密度；B和λ均为材料常数。
将相关参数代入模型进行拟合,得到如图11所示的非弹性应变能密度与疲劳寿命之间的关系,其拟合参数B为556.814,λ为-0.746,拟合相关系数为0.957 14,证明该模型对316L不锈钢不同条件下的疲劳寿命拟合效果较好。
![]()
图 11 不同试验条件下316L不锈钢疲劳寿命的能量法模型拟合结果Figure 11. Fitting results of energy mothod model for 316L stainless steel fatigue life under different conditions3.2 模型的对比
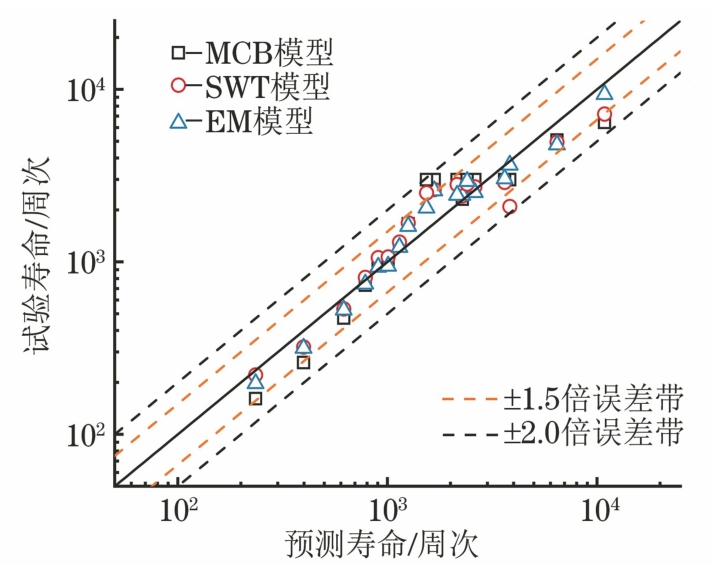
将不同试验条件下的疲劳寿命试验结果与不同模型预测结果进行对比。由图12可见：不同试验条件下3种模型的预测结果均在2倍误差带内,其中EM模型在小误差方面表现出显著优势,预测结果位于1.5倍误差带内。
![]()
图 12 不同试验条件下316L不锈钢的疲劳寿命试验结果与不同模型预测结果的散点图Figure 12. Scatter plot of fatigue life test results and different model prediction results of 316L stainless steel under different test conditions采用概率密度函数（PDF）对寿命预测模型的预测误差Perror进行分析,表达式[34]为
(9) 式中：Np,Ne分别为预测寿命和试验寿命。
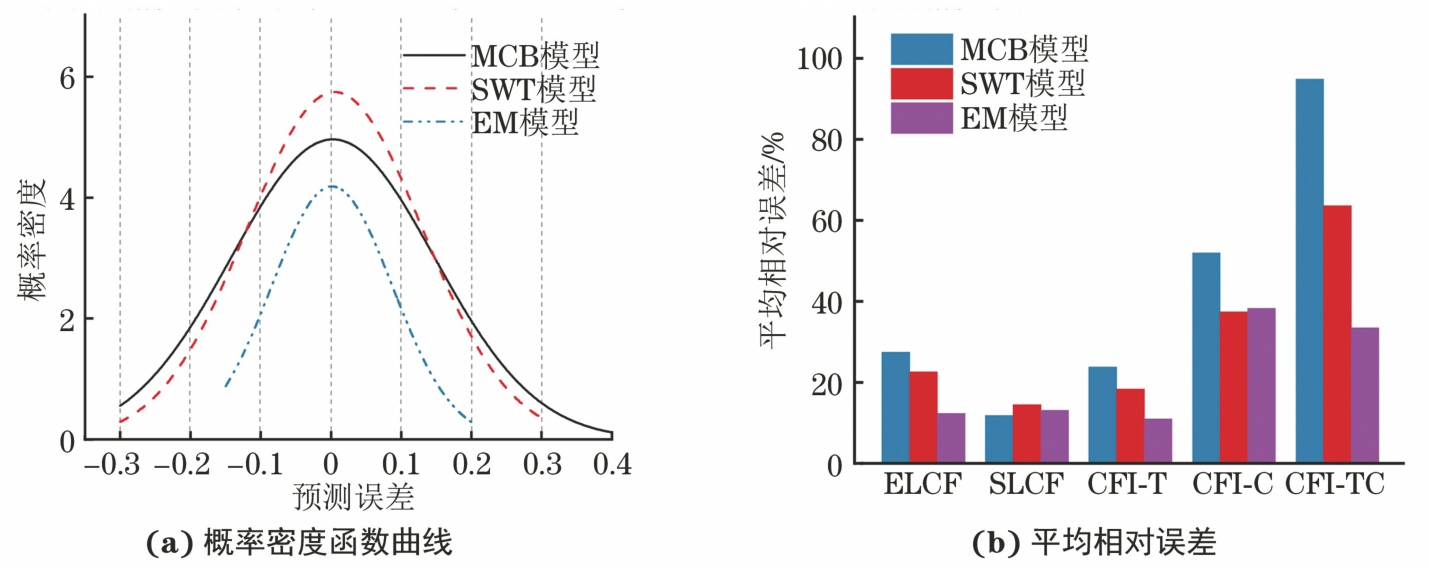
通过式（9）计算出预测误差,采用Origin软件进行正态分布拟合,得到概率密度函数曲线。为综合评估不同模型对不同循环载荷下试验钢疲劳寿命的预测能力,采用预测寿命与试验寿命之间的平均相对误差进行衡量。由图13可以看出：相较于MCB模型和SWT模型,EM模型的概率密度函数曲线更窄,说明该模型的预测误差离散程度最小；MCB模型和SWT模型对CFI-TC试验下的疲劳寿命预测效果差,相对误差最高,分别为94.86%,63.57%,EM模型对CFI-C试验下的疲劳寿命预测精度最差,相对误差最大为38.28%,同时在5种试验条件下EM模型的平均相对误差均最小。综上,EM模型对316L不锈钢在不同控制模式下的疲劳寿命预测精度最高,其次是SWT模型,MCB模型的预测精度最低。
![]()
图 13 316L不锈钢不同疲劳寿命预测模型的概率密度函数曲线以及在不同试验条件下疲劳寿命的平均相对误差Figure 13. Probability density function curves (a) of different fatigue life prediction models for 316L stainless steel and average relative error of fatigue life under different test conditions (b)4. 结论
（1）在不同控制模式的疲劳循环载荷下,316L不锈钢的循环应力响应均包括循环硬化、循环软化和失效断裂3个阶段。
（2）在应变控制低周疲劳和应力控制低周疲劳试验中,316L不锈钢的疲劳寿命随应变幅或应力幅的增大而缩短；在应变控制蠕变疲劳试验中,其疲劳寿命随拉伸保载时间的延长而缩短,随压缩保载时间的延长而增大,这与动态应变时效和蠕变对疲劳损伤的综合作用有关。在相同保载时间下,压缩保载下的疲劳寿命比拉伸保载下的短,这与不同加载方式引起的氧化层致裂机制有关。
（3）在MCB模型、SWT模型和EM模型中,EM模型的概率密度函数曲线最窄,预测误差分散性最小,EM模型对不同试验条件下疲劳寿命预测值的平均相对误差均最小,预测精度在1.5倍误差带以内,预测精度最高,MCB模型的预测精度最低。
-
![]()
图 3 316L不锈钢在不同试验条件下的峰值应力/应变与循环次数的关系曲线
Figure 3. Peak stress/strain vs cycle number curves of 316L stainless steel under different test conditions
![]()
图 4 316L不锈钢在不同控制模式低周疲劳试验下的循环塑性应变比与循环次数的关系曲线
Figure 4. Curves of cyclic plastic strain ratio vs cycle number of 316L stainless steel after low cycle fatigue tests under different control modes
![]()
图 5 316L不锈钢在不同控制模式低周疲劳试验下半寿命时的应力-应变滞回曲线
Figure 5. Stress-strain hysteresis curves of 316L stainless steel at half life after low cycle fatigue tests under different control modes
![]()
图 6 316L不锈钢在CFI-T和CFI-CT试验下半寿命时的应力-应变滞回曲线和应力松弛曲线
Figure 6. Stress-strain hysteresis curves (a) and stress relaxation curves (b) of 316L stainless steel at half life under CFI-T and CFI-CT tests
![]()
图 7 316L不锈钢在CFI-C和CFI-CT试验下半寿命时的应力-应变滞回曲线和应力松弛曲线
Figure 7. Stress-strain hysteresis curves (a) and stress relaxation curves (b) of 316L stainless steel at half life under CFI-C and CFI-CT tests
![]()
图 8 不同试验条件下316L不锈钢的非弹性应变能密度变化曲线
Figure 8. Inelastic strain energy density curves of 316L stainless steel under different test conditions
![]()
图 9 316L不锈钢疲劳寿命的MCB模型、Basquin模型、Manson-Coffin模型拟合结果
Figure 9. Fitting results of MCB model, Basquin model and Manson-Coffin model for 316L stainless steel fatigue life
![]()
图 10 不同试验条件下316L不锈钢疲劳寿命的SWT模型拟合结果
Figure 10. Fitting results of SWT model for 316L stainless steelfatigue life under different conditions
![]()
图 11 不同试验条件下316L不锈钢疲劳寿命的能量法模型拟合结果
Figure 11. Fitting results of energy mothod model for 316L stainless steel fatigue life under different conditions
![]()
图 12 不同试验条件下316L不锈钢的疲劳寿命试验结果与不同模型预测结果的散点图
Figure 12. Scatter plot of fatigue life test results and different model prediction results of 316L stainless steel under different test conditions
![]()
图 13 316L不锈钢不同疲劳寿命预测模型的概率密度函数曲线以及在不同试验条件下疲劳寿命的平均相对误差
Figure 13. Probability density function curves (a) of different fatigue life prediction models for 316L stainless steel and average relative error of fatigue life under different test conditions (b)
表 1 316L不锈钢的化学成分
Table 1 Chemical composition of 316L stainless steel
元素 C Mn P S Si Ni Cr Mo 质量分数/% 0.031 1.11 0.030 0.006 1 0.412 11.78 18.09 2.29 
下载: 导出CSV
表 2 316L不锈钢的拉伸性能
Table 2 Tensile properties of 316L stainless steel
温度/℃ 屈服强度/MPa 抗拉强度/MPa 断后伸长率/% 25 289 589 79.8 550 150 378 52.7
下载: 导出CSV
表 3 316L不锈钢在不同试验条件下的疲劳寿命试验值
Table 3 Fatigue life test values of 316L stainless steel under different test conditions
试验 应变幅/% 应力幅/MPa 保载时间/s 疲劳寿命/周次 ELCF 0.3 10 857 0.4 3 835 0.6 903 0.8 619 1.0 398 1.2 235 SLCF 230 6 437 250 2 276 270 1 257 280 1 142 290 1 007 300 784 CFI-T 60 3 624 0.4 180 2 613 600 2 148 CFI-C 0.4 60 1 672 180 2 401 CFI-TC 0.4 180 1 537
下载: 导出CSV
-
[1] CHEN G, ZHANG Y, XU D K, et al. Low cycle fatigue and creep-fatigue interaction behavior of nickel-base superalloy GH4169 at elevated temperature of 650 ℃[J]. Materials Science and Engineering: A, 2016, 655: 175-182. [2] FAN Y N, SHI H J, TOKUDA K. A generalized hysteresis energy method for fatigue and creep-fatigue life prediction of 316L(N)[J]. Materials Science and Engineering: A, 2015, 625: 205-212. [3] ZHONG W H, TONG Z F, WANG C L, et al. Fatigue behavior of domestic 316LN stainless steel under simulated AP1000 primary coolant environment[J]. Atomic Energy Science and Technology, 2017, 51(10): 1846-1852. [4] YUAN X Y, YU W W, FU S C, et al. Effect of mean stress and ratcheting strain on the low cycle fatigue behavior of a wrought 316LN stainless steel[J]. Materials Science and Engineering: A, 2016, 677: 193-202. [5] WALKER C D. Paper 24: Strain-fatigue properties of some steels at 950 ℉ (510 ℃) with a hold in the tension part of the cycle[J]. Proceedings of the Institution of Mechanical Engineers, Conference Proceedings, 1963, 178(1): 3-49. [6] WANG X W, ZHANG W, GONG J M, et al. Low cycle fatigue and creep fatigue interaction behavior of 9Cr-0.5Mo-1.8W-V-Nb heat-resistant steel at high temperature[J]. Journal of Nuclear Materials, 2018, 505: 73-84. [7] HORMOZI R, BIGLARI F, NIKBIN K. Experimental and numerical creep-fatigue study of Type 316 stainless steel failure under high temperature LCF loading condition with different hold time[J]. Engineering Fracture Mechanics, 2015, 141: 19-43. [8] 肖永健, 王勇, 井新经. P92钢在蠕变-疲劳交互作用下的初始循环特性[J]. 机械工程材料, 2022, 46(5): 88-94. XIAO Y J, WANG Y, JING X J. Initial cyclic characteristics of P92 steel under creep-fatigue interaction[J]. Materials for Mechanical Engineering, 2022, 46(5): 88-94.
[9] 王润梓, 廖鼎, 张显程, 等. 高温结构蠕变疲劳寿命设计方法: 从材料到结构[J]. 机械工程学报, 2021, 57(16): 66-86. WANG R Z, LIAO D, ZHANG X C, et al. Creep-fatigue life design methods in high-temperature structures: From materials to components[J]. Journal of Mechanical Engineering, 2021, 57(16): 66-86.
[10] SMITH K N, WATSON P, TOPPER T H. A stress-strain function for the fatigue of metals[J]. Journal of Materials, 1976(5): 767-778. [11] COLIN J, FATEMI A, TAHERI S. Fatigue behavior of stainless steel 304L including strain hardening, prestraining, and mean stress effects[J]. Journal of Engineering Materials and Technology, 2010, 132(2): 1. [12] SHANKAR V, SANDHYA R, MATHEW M D. Creep-fatigue-oxidation interaction in Grade 91 steel weld joints for high temperature applications[J]. Materials Science and Engineering: A, 2011, 528(29/30): 8428-8437. [13] TOTEMEIER T C, TIAN H B. Creep-fatigue-environment interactions in INCONEL 617[J]. Materials Science and Engineering: A, 2007, 468/469/470(12): 81-87. [14] HONG S G, LEE S B, BYUN T S. Temperature effect on the low-cycle fatigue behavior of type 316L stainless steel: Cyclic non-stabilization and an invariable fatigue parameter[J]. Materials Science and Engineering: A, 2007, 457(1/2): 139-147. [15] PRASAD REDDY G V, SANDHYA R, VALSAN M, et al. High temperature low cycle fatigue properties of 316(N) weld metal and 316L(N)/316(N) weld joints[J]. International Journal of Fatigue, 2008, 30(3): 538-546. [16] GANESH SUNDARA RAMAN S. Effect of prior cold work on the room-temperature low-cycle fatigue behaviour of AISI 304LN stainless steel[J]. International Journal of Fatigue, 1996, 18(2): 71-79. [17] HONG S. The effect of temperature on low-cycle fatigue behavior of prior cold worked 316L stainless steel[J]. International Journal of Fatigue, 2003, 25(9/10/11): 1293-1300. [18] PAUL S K, SIVAPRASAD S, DHAR S, et al. Cyclic plastic deformation and cyclic hardening/softening behavior in 304LN stainless steel[J]. Theoretical and Applied Fracture Mechanics, 2010, 54(1): 63-70. [19] WU D L, ZHAO P, WANG Q Q, et al. Cyclic behavior of 9-12% Cr steel under different control modes in low cycle regime: A comparative study[J]. International Journal of Fatigue, 2015, 70: 114-122. [20] MIGUEL M C, VESPIGNANI A, ZAPPERI S, et al. Intermittent dislocation flow in viscoplastic deformation[J]. Nature, 2001, 410(6829): 667-671. [21] PHAM M S, HOLDSWORTH S R. Dynamic strain ageing of AISI 316L during cyclic loading at 300 ℃: Mechanism, evolution, and its effects[J]. Materials Science and Engineering: A, 2012, 556: 122-133. [22] JINRUI H, DUAN Z X, NING Y L. Strain energy partitioning and its application to GH33A Ni-base superalloy and 1Cr18Ni9Ti stainless steel[J]. Acta Metallurgica Sinica, 1985, 21: 54-63. [23] FELTHAM P. Creep and stress relaxation in alpha-brass at low temperatures[J]. Philosophical Magazine, 1961, 6(62): 259-270. [24] AOTO K, KOMINE R, UENO F, et al. Creep-fatigue evaluation of normalized and tempered modified 9Cr-1Mo[J]. Nuclear Engineering and Design, 1994, 153(1): 97-110. [25] HONG S G, LEE S B. Mechanism of dynamic strain aging and characterization of its effect on the low-cycle fatigue behavior in type 316L stainless steel[J]. Journal of Nuclear Materials, 2005, 340(2/3): 307-314. [26] LI B B, ZHENG Y M, ZHAO J W, et al. Cyclic deformation behavior and dynamic strain aging of 316LN stainless steel under low cycle fatigue loadings at 550 ℃[J]. Materials Science and Engineering: A, 2021, 818: 141411. [27] 杨佳东, 朱鉴, 周强, 等. 保载时间对P92 蠕变-疲劳交互行为的影响[J]. 压力容器, 2022, 39(1): 1-8. YANG D J, ZHU J, ZHOU Q et al. Experimental investigation on effect of holding time on creep-fatigue behaviors of P92 steel[J]. Pressure Vessel Technology, 2022, 39(1): 1-8.
[28] MANSON S S. Behavior of materials under conditions of thermal stress[M]. Washington, D. C.: National Advisory Committee for Aeronautics, 1953. [29] COFFIN J L F. Predictive parameters and their application to high temperature, low cycle fatigue[J]. Fracture London Chapman & Hal, 1969, 56: 1-12. [30] CONCER D, WOELLNER N, MARCONDES P. Approach to the prediction of thermal fatigue of aluminium high pressure die casting (AlSI H13) using the Basquin equation and finite elements[J]. Journal of Achievements in Materials and Manufacturing Engineering, 2012, 55(2): 439-445. [31] 田阳, 陈巍峰, 赵姿贞, 等. 应变比对2. 25Cr1MoV钢高温低周疲劳行为的影响[J]. 机械工程材料, 2015, 39(11): 83-87. TIAN Y, CHEN W F, ZHAO Z Z, et al. Effect of strain ratio on low cycle fatigue behavior of 2.25Cr1MoV steel at high temperature[J]. Materials for Mechanical Engineering, 2015, 39(11): 83-87.
[32] TONG X Y, WANG D J, XU H. Investigation of cyclic hysteresis energy in fatigue failure process[J]. International Journal of Fatigue, 1989, 11(5): 353-359. [33] KUJAWSKI D, ELLYIN F. A cumulative damage theory for fatigue crack initiation and propagation[J]. International Journal of Fatigue, 1984, 6(2): 83-88. [34] ZHANG T Y, WANG X W, JI Y N, et al. P92 steel creep-fatigue interaction responses under hybrid stress-strain controlled loading and a life prediction model[J]. International Journal of Fatigue, 2020, 140: 105837.
计量
- 文章访问数: 137
- HTML全文浏览量: 8
- PDF下载量: 26
