Page 79 - 电力与能源2021年第八期

张思源, 等: 光伏并网系统的谐波谐振评估与安全防控 4 5
4
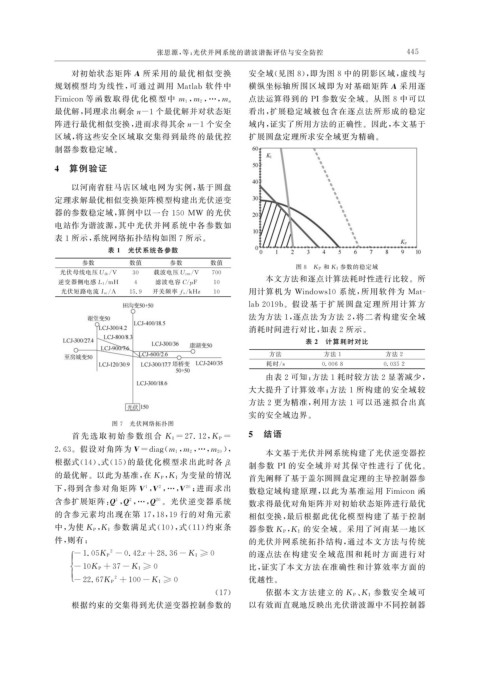
对初始状态矩阵 A 所采用的最优相似变换 安全域( 见图 8 ), 即为图 8 中的阴影区域, 虚线与
规划模型均 为线 性, 可 通 过 调 用 Matlab 软 件 中 横纵坐标轴所围区域即为对基础矩阵 A 采用逐
点法运算得到的 PI参数安全域。从图 8 中可以
, ,…, m n
Fimicon等 函 数 取 得 优 化 模 型 中 m 1 m 2
最优解, 同理求出剩余n-1 个最优解并对状态矩 看出, 扩展稳定域被包含在逐点法所形成的稳定
阵进行最优相似变换, 进而求得其余n-1 个安全 域内, 证实了所用方法的正确性。因此, 本文基于
区域, 将这些安全区域取交集得到最终的最优控 扩展圆盘定理所求安全域更为精确。
制器参数稳定域。

4 算例验证

以河南省驻马店区域电网为实例, 基于圆盘
定理求解最优相似变换矩阵模型构建出光伏逆变
器的参数稳定域, 算例中以一台 150 MW 的光伏
电站作为谐波源, 其中光伏并网系统中各参数如
表 1 所示, 系统网络拓扑结构如图 7 所示。
表 1 光伏系统各参数
参数 数值 参数 数值
图 8 K P 和 K I 参数的稳定域
光伏母线电压Udc / V 30 载波电压U cm / V 700
本文方法和逐点计算法耗时性进行比较。所
逆变器侧电感 L 1 / mH 4 滤波电容 C / F 10
μ
光伏短路电流I sc / A 15.9 开关频率 f s / kHz 10 用计算机为 Windows10 系统, 所用软件为 Mat-
lab2019b 。假设基于扩展圆盘定理所用计算方
法为方法 1 , 逐点法为方法 2 , 将二者构建安全域
消耗时间进行对比, 如表 2 所示。
表 2 计算耗时对比
方法 方法 1 方法 2
耗时 / s 0.0068 0.0352
由表 2 可知: 方法 1 耗时较方法 2 显著减少,
大大提升了计算效率; 方法 1 所构建的安全域较
方法 2 更为精准, 利用方法 1 可以迅速拟合出真
实的安全域边界。
图 7 光伏网络拓扑图
5 结语
首 先 选 取 初 始 参 数 组 合 K I=27.12 , K P =
),
( , ,…, m 20
2.63 。假设对角阵为V=dia g m 1 m 2 本文基于光伏并网系统构建了光伏逆变器控
根据式( 14 )、 式( 15 ) 的最优化模型求出此时各
β i 制参数 PI的安全域并对其保守性进行了优化。
的最优解。以此为基准, 在 K P K I 为变量的情况 首先阐释了基于盖尔圆圆盘定理的主导控制器参
,
下, 得到含参对角矩阵 V , V ,…, V ; 进而求出 数稳定域构建原理, 以此为基准运用 Fimicon 函
1
20
2
含参扩展矩阵: , ,…, 20 。光伏逆变器系统 数求得最优对角矩阵并对初始状态矩阵进行最优
Q Q
1
2
Q
的含参元素均出现在第 17 , 18 , 19 行的对角元素 相似变换, 最后根据此优化模型构建了基于控制
中, 为使 K P K I 参数满足式( 10 ), 式( 11 ) 约束条 器参数 K P K I 的安全域。采用了河南某一地区
,
,
件, 则有: 的光伏并网系统拓扑结构, 通过本文方法与传统
2 的逐点法在构建 安全域范围和耗时方面进行对
ì -1.05K P -0.42 x+28.36-K I ≥0
ï
ï
í -10 K P +37-K I ≥0 比, 证实了本文方法在准确性和计算效率方面的
ï ï
î -22.67K P +100-K I ≥0 优越性。
2
( 17 ) 依据本文方法建立的 K P K I 参数安全域可
、
根据约束的交集得到光伏逆变器控制参数的 以有效而直观地反映出光伏谐波源中不同控制器