Page 84 - 电力与能源2024年第二期

224 孙玉波，等：基于 GA-PSO-BP 与灰色关联的光伏短期功率预测

优值，而 GA 与 PSO 算法分别在第 98 次与第 97 次
才找到最优值。3 种算法的性能比较见表 1。
表 1 3 种算法的性能比较
陷入局部最优 接近最优
算法类型 最优值
次数/次 次数/次
PSO 0.004 7 52 48
GA 0.004 8 20 80
GA⁃PSO 0.003 1 8 92
由表 1 可知，PSO 算法在 100 次迭代中，有 52
次陷入了局部最优，未能找到全局最优；GA 算法
相比 PSO 算法陷入局部最优的次数明显减少，有
利于算法求得最优解；本文提出的 GA-PSO 算法

继承了 GA 算法跳出局部最优的能力，在寻优精
度上有了进一步提升，求得最优解的次数也明显
增加。
4.2 实际光伏功率预测
本文选取 2017 年江苏某地区 1 月至 3 月 7：00
−17：00 时间段的光伏数据，每 15 min 作为一个
采样点，选取太阳辐照度、环境温度、环境湿度以
及实际发出的功率数据作为一个样本，每天总共

41 个点。
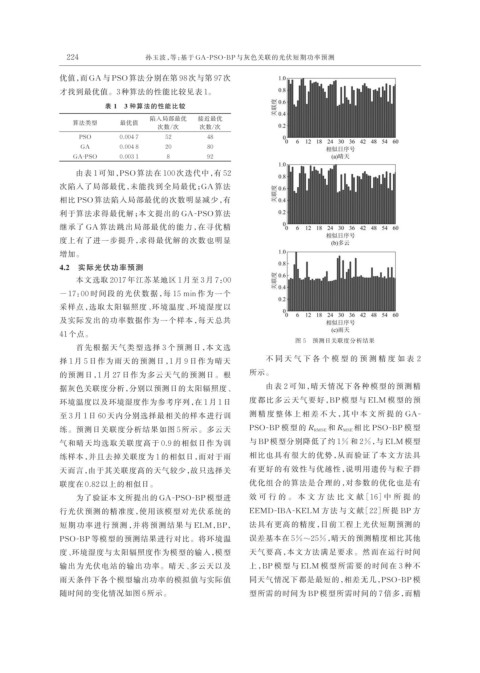
图 5 预测日关联度分析结果
首先根据天气类型选择 3 个预测日，本文选
择 1 月 5 日作为雨天的预测日，1 月 9 日作为晴天 不 同 天 气 下 各 个 模 型 的 预 测 精 度 如 表 2
的预测日，1 月 27 日作为多云天气的预测日。根 所示。
据灰色关联度分析，分别以预测日的太阳辐照度、 由表 2 可知，晴天情况下各种模型的预测精

环境温度以及环境湿度作为参考序列，在 1 月 1 日 度都比多云天气要好，BP 模型与 ELM 模型的预
至 3 月 1 日 60 天内分别选择最相关的样本进行训 测 精 度 整 体 上 相 差 不 大 ，其 中 本 文 所 提 的 GA-
练。预测日关联度分析结果如图 5 所示。多云天 PSO-BP 模型的 R RMSE 和 R MSE 相比 PSO-BP 模型
气和晴天均选取关联度高于 0.9 的相似日作为训 与 BP 模型分别降低了约 1% 和 2%，与 ELM 模型
练样本，并且去掉关联度为 1 的相似日，而对于雨 相比也具有很大的优势，从而验证了本文方法具
天而言，由于其关联度高的天气较少，故只选择关 有更好的有效性与优越性，说明用遗传与粒子群

联度在 0.82 以上的相似日。 优化组合的算法是合理的，对参数的优化也是有
为了验证本文所提出的 GA-PSO-BP 模型进 效 可 行 的 。 本 文 方 法 比 文 献［16］中 所 提 的
行光伏预测的精准度，使用该模型对光伏系统的 EEMD-IBA-KELM 方 法 与 文 献［22］所 提 BP 方
短期功率进行预测，并将预测结果与 ELM，BP， 法具有更高的精度，目前工程上光伏短期预测的
PSO-BP 等模型的预测结果进行对比。将环境温 误差基本在 5%~25%，晴天的预测精度相比其他

度、环境湿度与太阳辐照度作为模型的输入，模型 天气要高，本文方法满足要求。然而在运行时间
输出为光伏电站的输出功率。晴天、多云天以及 上，BP 模型与 ELM 模型所需要的时间在 3 种不
雨天条件下各个模型输出功率的模拟值与实际值 同天气情况下都是最短的，相差无几，PSO-BP 模
随时间的变化情况如图 6 所示。 型所需的时间为 BP 模型所需时间的 7 倍多，而精