Page 51 - 电力与能源2024年第三期
P. 51
吴张傲:110 kV 输电线路塔杆接地电阻检测算法研究 325
比较式(3)~(6)可知:
1 接地电阻测量方法
1 1 1
+ - = 0 (7)
1.1 接地电阻测量原理 L OP L OC L OC + L OP
若接地极呈现半球形,接地极周围电位均匀 式(6)无实数解,即电流极与电压极位于两侧
分布,则电场强度 E 可表示为 的方法无法正确地找到位置。
Iρ Iρ 电 压 极 与 电 流 极 位 于 同 侧 的 分 布 如 图 2
E = Jρ = = (1)
S 2πr 2 所示。
式中 J——电流密度;I——接地极电流;ρ——土
壤电阻率;S——半球面的面积。
无穷远处的接地极电位 U r 可表示为
r r
U r = ∫ - Edx = ∫ - Jρdx =
∞ ∞
r Iρ Iρ Iρ
r
∫ - dx = | ∞ = (2)
∞ 2πr 2 2πr 2πr
进而可得位于 r o 处的接地极电阻:
图 2 电压极与电流极位于同侧的分布
ρ
R 0 = (3) 电流极与电压极的距离应满足式(8)。
2πr 0
1 1 1
1.2 三极法测量接地电阻 + - = 0 (8)
利用三极法测量接地电阻时,需在接地极附 L OP L OC L PC
式中 L PC——电压极与电流极之间的距离。
近安装两个辅助极,分别为电压极与电流极,其分
测量电阻的误差 ε 可表示为
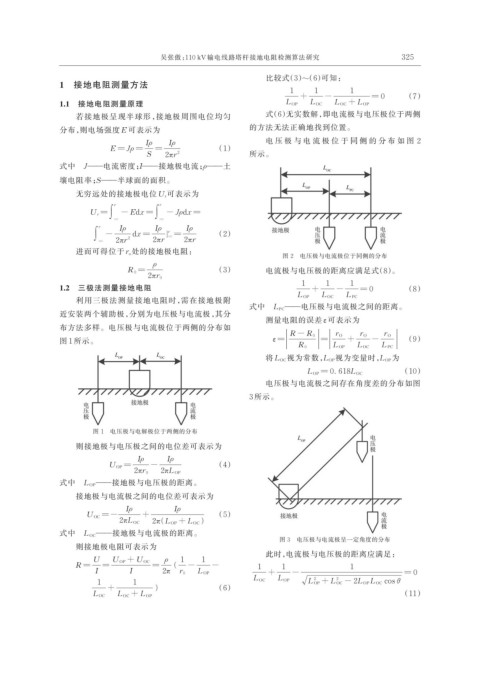
布方法多样。电压极与电流极位于两侧的分布如 | | | R - R 0 | | | r O | | |
|
r O
图 1 所示。 ε =| | | R 0 | |=| | | | r O + L OC - L PC | | | (9)
|
| L OP
将 L OC 视为常数,L OP 视为变量时,L OP 为
(10)
L OP = 0. 618L OC
电压极与电流极之间存在角度差的分布如图
3 所示。
图 1 电压极与电解极位于两侧的分布
则接地极与电压极之间的电位差可表示为
Iρ Iρ
U OP = - (4)
2πr 0 2πL OP
式中 L OP——接地极与电压极的距离。
接地极与电流极之间的电位差可表示为
Iρ Iρ
U OC =- + (5)
2π( L OP + L OC )
2πL OC
式中 L OC——接地极与电流极的距离。
图 3 电压极与电流极呈一定角度的分布
则接地极电阻可表示为
此时,电流极与电压极的距离应满足:
U U OP + U OC ρ 1 1
R = = = ( - - 1 1 1
I I 2π r 0 L OP + - = 0
2
2
1 1 L OC L OP L OP + L OC - 2L OP L OC cos θ
+ ) (6)
L OC L OC + L OP (11)