Page 69 - 电力与能源2022年第一期

郭强强, 等: 光储充一体化电站优化配置方法 6
3
n
( 1+ r )
(
)
C ESS = E rate C E +P rate C P · [ ( 1+ r ) -1 + α ] 在阶段 t 的最小和最大输出功率, 与当前阶段储
n
能系统的 SOC 值、 SOC 上下限及额定功率相关;
( 10 )
P ESSt ,
()———阶段 t储能系统的输出功率; SOC i , max
———储能系 统的单位 容 量 价 格, 万 元 /
式中 C E ———第i 个 储 能 系 统 SOC 上 下 限 值;
SOC i , min
———储 能 系 统 的 额 定 功 率, MW ;
SOC it
MWh ; P rate ()———阶段 t储能系统的值。
———储能 系 统 的 单 位 功 率 价 格, 万 元 / MW ;
C P
3 算例分析
n ———储能 系 统 的 使 用 寿 命, 年; r ———年 利 率;
α ———运维费用率。 3.1 算例参数
2 优化配置模型 本文以 某 光 储 充 一 体 化 电 站 为 例, 共 配 置
12 台60kW 快充桩, 配变容量800kVA , 以1 回
2.1 优化目标 10kV 线路接 入 系 统。根 据 光 储 充 一 体 化 能 源
设备模型中已经得到储能系统的收益和成本 站屋顶面 积 和 剩 余 空 间, 设 定 光 伏 安 装 容 量 上
计算方法, 光储充一体化电站配置的优化目标为
限为 2000kW , 储能装机容量上限为 1000k W
最大化电站的净收益, 如下式:
×2h 。
T
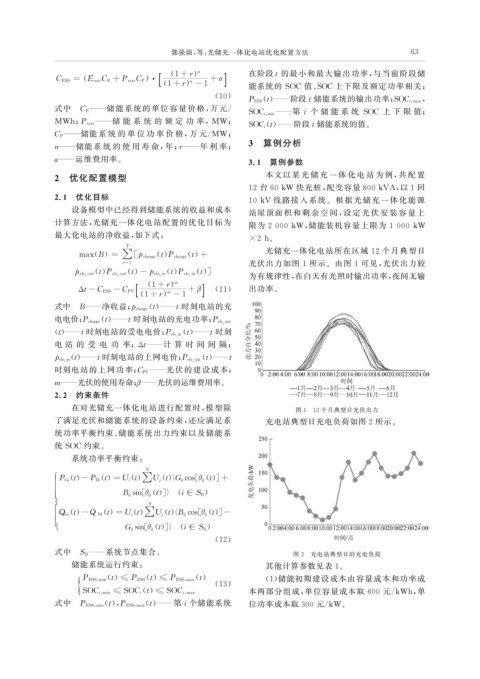
光储充一体化电站所在区域 12 个月典型日
max ( B ) = ∑ [ () ()
p char g etP char g et +
t = 1 光伏出力如图 1 所示。由图 1 可见, 光伏出力较
(
(
(
(
p ele _ outt ) P ele _ outt ) -p ele _ int ) P ele _ int )]
为有规律性, 在白天有光照时输出功率, 夜间无输
m
Δ t-C ESS -C PV[ ( 1+ r ) + β] ( 11 ) 出功率。
m
( 1+ r ) -1
p char g et
式中 B ———净收益; ()——— t时刻电站的充
(
电电价; P char g et )——— t时刻电站的充电功率; P ele _ out
()——— t时刻
( t )——— t时刻电站的受电电价; P ele _ in t
电 站 的 受 电 功 率; Δ t ———计 算 时 间 间 隔;
(
p ele _ int )——— t时刻电站的上网电价; P ele _ outt )——— t
(
———光伏的建设成本;
时刻电站的上网功率; C PV
m ———光伏的使用寿命;———光伏的运维费用率。
β
2.2 约束条件
在对光储充一体化电站进行配置时, 模型除 图 1 12 个月典型日光伏出力
了满足光伏和储能系统的设备约束, 还应满足系 充电站典型日充电负荷如图 2 所示。
统功率平衡约束、 储能系统出力约束以及储能系
统 SOC 约束。
系统功率平衡约束:
N
ì P Git -P Dit =U it ∑ (){ ()]
() U jt G i j cos [ θ i j t +
()
()
ï
ï
ï ï B i j sin [ θ i j t )
()]} ( i∈S B
í N
ï Q Git -Q Dit =U it (){ ()]
()
() U jt B i j cos [ θ i j t -
()
ï ∑
ï
î G i j sin [ θ i j t )
()]} ( i∈S B
( 12 )
———系统节点集合。
式中 S B 图 2 充电站典型日的充电负荷
储能系统运行约束: 其他计算参数见表 1 。
()
()
()
{ P ESS , mint ≤P ESS t ≤P ESS , maxt ( 13 ) ( 1 ) 储能初期建设成本由容量成本和功率成
()
SOC i , min ≤SOC it ≤SOC i , max 本两部分组成, 单位容量成本取 600 元 / kWh , 单
()———第i个储能系统
式中 P ESS , mint P ESS , maxt 位功率成本取 300 元 / kW 。
(),