Page 46 - 电力与能源2022年第五期

4 0 8 彭 昕, 等: 基于密度的聚类算法与改进拉依达准则的 95598 工单处理方法

常点, 基本技术路线如图 2 所示。计算抄表段中
心坐标不易受离群异常点影响, 剔除异常点后也
有利于提升下一步先计算抄表段中心再识别异常
点的改进拉依达准则算法的鲁棒性。

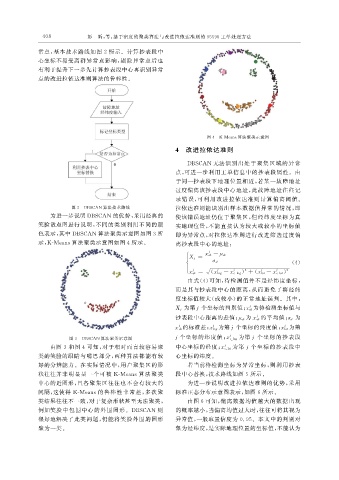
图 4 K-Means算法聚类示意图
4 改进拉依达准则

DBSCAN 无法识别出处于聚集区域的异常
点, 可进一步利用工单信息中的抄表段属性。由
于同一抄表段下地理位置相近, 若某一故障地址
过度偏离该抄表段中心地址, 此故障地址往往记
录错误, 可利用改进拉依达准则计算偏离阈值。
图 2 DBSCAN 算法技术路线 拉依达准则能识别出样本数据值异常的情况, 即
为进一步说明 DBSCAN 的优势, 采用经典的 使该错误地址仍位于聚集区, 但经纬度坐标为真
笑脸散点图进行说明, 不同的类别利用不同的颜 实地理位置, 不能直接认为较大或较小的坐标值
色表示, 其中 DBSCAN 算法聚类示意图如图3 所 即为异常点, 对拉依达准则进行改进筛选过度偏
示, K-Means算法聚类示意图如图 4 所示。 离抄表段中心的地址:
j
ì X j = x di - μ di
ï
ï
í σ d ( 4 )
ï ï
î x di = ( x ln g -x c _ ln g ) + x lat-x c _ lat )
j
j
j
j
j
2
2
(
由式( 4 ) 可知, 待检测值并不是经纬度坐标,
而是其与抄表段中心的距离, 从而避免了将经纬
度坐标值较大( 或较小) 的正常地址误判。其中:
为第 j 个坐标的判别值; x di 为待检测坐标值与
j
X j
j
抄表段中心距离的差值; 为x di 的平均值; σ d 为
μ di
j
j j 为第 j 个坐标的经度值; x lat 为第
x di 的标准差; x ln g
j 为第 j 个坐标的抄表段
图 3 DBSCAN 算法聚类示意图 j 个坐标的纬度值; x c _ ln g
由图 3 和图 4 可知, 对于相对而言较容易聚 中心坐标的经度; x c _ lat 为第 j 个坐标的抄表段中
j
类的笑脸的眼睛与嘴巴部分, 两种算法都能有较 心坐标的纬度。
好的分辨能力。在实际情况中, 用户聚集区的形 若当前待检测坐标为异常坐标, 则利用抄表
状往往并非明显呈一个可被 K-Means 算法聚类 段中心替换, 技术路线如图 5 所示。
中心的近圆形, 且各聚集区往往也不会有较大的 为进一步说明改进拉依达准则的优势, 采用
间隔, 这使得 K-Means的鲁棒性非常差, 多次聚 标准正态分布示意图表示, 如图 6 所示。
类结果往往不一致, 对于复杂形状甚至无法聚类, 由图 6 可知, 偏离数据均值越大的数据出现
例如笑脸中包围中心的外围圆形。 DBSCAN 则 的概率越小, 当偏离均值过大时, 往往可将其视为
很好地解决了此类问题, 仍能将笑脸外围的圆形 异常值, 一般取置信度为 0.95 。本文中的判别对
聚为一类。 象为经纬度, 是实际地理位置的坐标值, 不能认为