Page 60 - 电力与能源2024年第二期

200 朱长东，等：电力电缆温升特性研究及载流量计算

为了实现这一目标，使用 MATLAB 和 COMSOL
进行联合仿真，以进行对目标函数 F 的迭代寻优。
整个迭代寻优过程如图 3 所示。

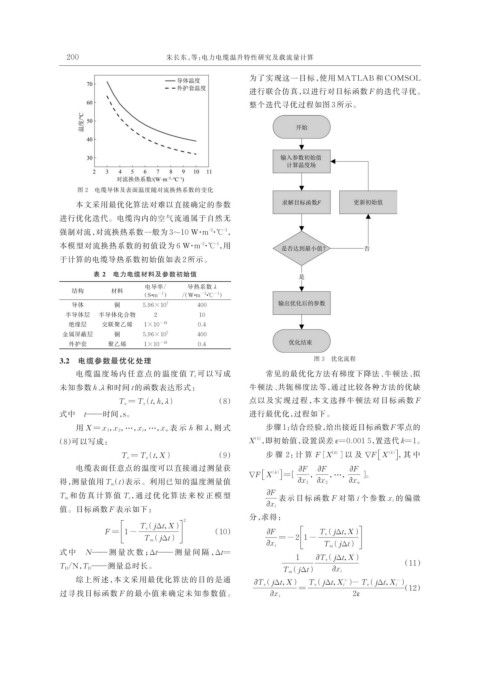
图 2 电缆导体及表面温度随对流换热系数的变化
本文采用最优化算法对难以直接确定的参数
进行优化迭代。电缆沟内的空气流通属于自然无
强制对流，对流换热系数一般为 3~10 W·m ·℃ ，
-2
-1
本模型对流换热系数的初值设为 6 W·m ·℃ ，用
-2
-1
于计算的电缆导热系数初始值如表 2 所示。
表 2 电力电缆材料及参数初始值
电导率/ 导热系数 λ
结构 材料
（S·m ） /（W·m -2 ·℃ ）
-1
-1
导体 铜 5.96×10 7 400
半导体层 半导体化合物 2 10
绝缘层 交联聚乙烯 1×10 -18 0.4
金属屏蔽层 铜 5.96×10 7 400
外护套 聚乙烯 1×10 -18 0.4

3.2 电缆参数最优化处理 图 3 优化流程
电缆温度场内任意点的温度值 T e 可以写成 常见的最优化方法有梯度下降法、牛顿法、拟
λ
未知参数 h、 和时间 t的函数表达形式： 牛顿法、共轭梯度法等，通过比较各种方法的优缺
T e = T e ( t，h，λ ) （8） 点以及实现过程，本文选择牛顿法对目标函数 F
式中 t——时间，s。 进行最优化，过程如下。

用 X = x 1，x 2，…，x i，…，x n 表 示 h 和 λ，则 式 步骤 1：结合经验，给出接近目标函数 F 零点的
（1）
（8）可以写成： X ，即初始值，设置误差 ε=0.001 5，置迭代 k=1。
（k）
T e = T e ( t，X ) （9） 步 骤 2：计 算 F［X ］以 及 ∇F[ X ( k ) ]，其 中
电缆表面任意点的温度可以直接通过测量获 ∂F ∂F ∂F
∇F[ X ( k ) ] =[ ， ，⋯， ]。
得，测量值用 T m （t）表示。利用已知的温度测量值 ∂x 1 ∂x 2 ∂x n
∂F
T m 和 仿 真 计 算 值 T e，通 过 优 化 算 法 来 校 正 模 型 表示目标函数 F 对第 i 个参数 x i 的偏微
∂x i
值。目标函数 F 表示如下：
分，求得：
é ê ê T e ( jΔt，X ú ú ù ) 2
F = 1 - ú ú （10） ∂F é ê ê T e ( jΔt，X ú ú ù )
ê ê
ê ê
ë T m ( jΔt ) û =-2 1 - ú ú
∂x i ë T m ( jΔt ) û
式 中 N—— 测 量 次 数 ； Δt—— 测 量 间 隔 ， Δt=
1 ∂T e ( jΔt，X )
T D/N，T D——测量总时长。 （11）
T m ( jΔt ) ∂x i
综上所述，本文采用最优化算法的目的是通 + -
∂T e ( jΔt，X ) T e ( jΔt，X i )- T e ( jΔt，X i )
= （12）
过寻找目标函数 F 的最小值来确定未知参数值。 ∂x i 2ε