Page 61 - 电力与能源2024年第二期

朱长东，等：电力电缆温升特性研究及载流量计算 201

-
T e （jDt，X i ）和 T e （jDt，X i ）的值均由电缆温度
+
场计算得到，其中，X i =［x 1，x 2，…，x i+ε，…，xn］，
+
-
X i =［x 1，x 2，…，x i−ε，…，x n ］。
步骤 3：计算迭代公式。
F[ X ( k ) ]
( k + 1 ) ( k ) （13）
x i = x i -
( k ) ]
∇F[ X i
( k ) ]——第 k 次迭代中目标函数 F 对
式中 ∇F[ X i
第 i个参数的偏微分。
( k )
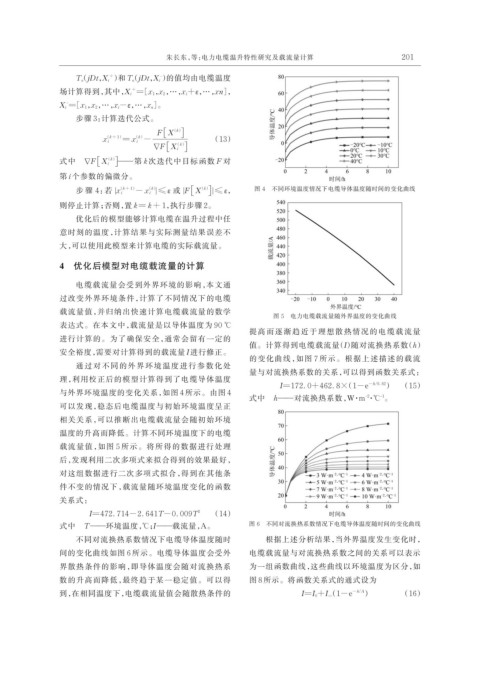
( k + 1 ) - x i | ≤ ε 或 |F[ X ( k ) 图 4 不同环境温度情况下电缆导体温度随时间的变化曲线
步 骤 4：若 |x i ]| ≤ ε，
则停止计算；否则，置 k = k + 1，执行步骤 2。
优化后的模型能够计算电缆在温升过程中任
意时刻的温度，计算结果与实际测量结果误差不
大，可以使用此模型来计算电缆的实际载流量。

4 优化后模型对电缆载流量的计算

电缆载流量会受到外界环境的影响，本文通
过改变外界环境条件，计算了不同情况下的电缆
载流量值，并归纳出快速计算电缆载流量的数学
图 5 电力电缆载流量随外界温度的变化曲线
表达式。在本文中，载流量是以导体温度为 90 ℃
提高而逐渐趋近于理想散热情况的电缆载流量
进行计算的。为了确保安全，通常会留有一定的
值。计算得到电缆载流量（I）随对流换热系数（h）
安全裕度，需要对计算得到的载流量 I 进行修正。
的变化曲线，如图 7 所示。根据上述描述的载流
通过对不同的外界环境温度进行参数化处
量与对流换热系数的关系，可以得到函数关系式：
理，利用校正后的模型计算得到了电缆导体温度
I=172. 0+462. 8×（1-e -h/6. 82 ） （15）
与外界环境温度的变化关系，如图 4 所示。由图 4
式中 h——对流换热系数，W·m ·℃ 。
-1
-2
可以发现，稳态后电缆温度与初始环境温度呈正
相关关系，可以推断出电缆载流量会随初始环境
温度的升高而降低。计算不同环境温度下的电缆

载流量值，如图 5 所示。将所得的数据进行处理
后，发现利用二次多项式来拟合得到的效果最好，
对这组数据进行二次多项式拟合，得到在其他条
件不变的情况下，载流量随环境温度变化的函数
关系式：
I=472. 714-2. 641T-0. 009T 2 （14）
式中 T——环境温度，℃；I——载流量，A。 图 6 不同对流换热系数情况下电缆导体温度随时间的变化曲线

不同对流换热系数情况下电缆导体温度随时 根据上述分析结果，当外界温度发生变化时，
间的变化曲线如图 6 所示。电缆导体温度会受外 电缆载流量与对流换热系数之间的关系可以表示
界散热条件的影响，即导体温度会随对流换热系 为一组函数曲线，这些曲线以环境温度为区分，如
数的升高而降低，最终趋于某一稳定值。可以得 图 8 所示。将函数关系式的通式设为
到，在相同温度下，电缆载流量值会随散热条件的 I=I 0+I ∞ （1-e -h/A ） （16）