Page 51 - 电力与能源2024年第五期

方 苏，等：基于梯度下降连续优化算法的线束截面布局优化设计方法 583

4）根据梯度的方向更新参数的值。参数更新
公式为

x = x - ρ∂U ( y i，y i )/∂x i （16）
y = y - ρ∂U ( x i，y i )/∂y i （17）
式中 ρ——学习率，控制每一步的更新步长。

5）更新参数后，再次计算 U（X k+1 ）的能量值
W（X k+1 ），如果
|W（X k+1 ）－W（X k ）|＜ δ，|x k+1－x k|＜ σ，或 者
|y k+1－y k|＜σ，或者迭代次数达上限 m，则停止迭代
搜 索 ，输 出 此 时 的 布 局 X*（x 1*，y 1*，x 2*，y 2*，… ，
y
x n*， n*）。
６）否则，ｋ＝ｋ＋１，转到步骤（4）继续迭代

搜索；
７）输出布局U（X）的弹性势能极小值W（X） min、
布局 X* （x 1*，y 1*，x 2*，y 2*，…，x n*，y n*）的具体坐标
以及迭代次数 m 等。
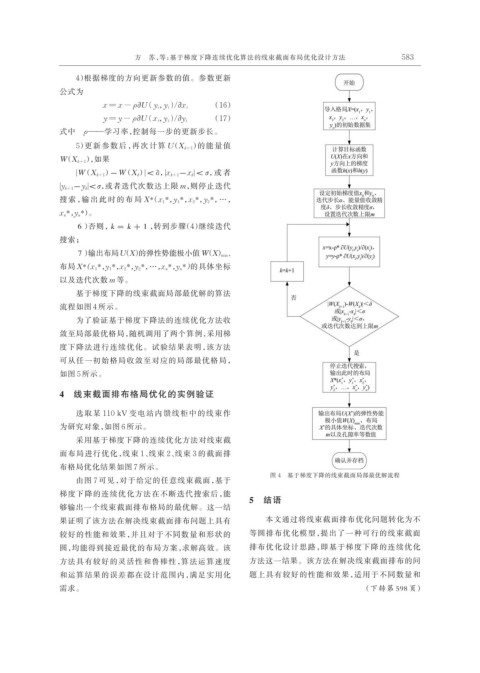
基于梯度下降的线束截面局部最优解的算法
流程如图 4 所示。
为了验证基于梯度下降法的连续优化方法收

敛至局部最优格局，随机调用了两个算例，采用梯
度下降法进行连续优化。试验结果表明，该方法
可从任一初始格局收敛至对应的局部最优格局，
如图 5 所示。

4 线束截面排布格局优化的实例验证

选取某 110 kV 变电站内馈线柜中的线束作
为研究对象，如图 6 所示。

采用基于梯度下降的连续优化方法对线束截
面布局进行优化，线束 1、线束 2、线束 3 的截面排
布格局优化结果如图 7 所示。
图 4 基于梯度下降的线束截面局部最优解流程
由图 7 可见，对于给定的任意线束截面，基于
梯度下降的连续优化方法在不断迭代搜索后，能
5 结语
够输出一个线束截面排布格局的最优解。这一结
果证明了该方法在解决线束截面排布问题上具有 本文通过将线束截面排布优化问题转化为不

较好的性能和效果，并且对于不同数量和形状的 等圆排布优化模型，提出了一种可行的线束截面
圆，均能得到接近最优的布局方案，求解高效。该 排布优化设计思路，即基于梯度下降的连续优化
方法具有较好的灵活性和鲁棒性，算法运算速度 方法这一结果。该方法在解决线束截面排布的问
和运算结果的误差都在设计范围内，满足实用化 题上具有较好的性能和效果，适用于不同数量和
需求。 （下转第 598 页）