Page 34 - 电力与能源2024年第五期

566 戴 金：基于最小二乘支持向量机的新型电力系统谐波分量预测

2.2 预测模型参数优化
3 结果分析
LSSVM 训练模型的预测精度与模型参数设
置紧密相关，而最优参数通常难以人工确定。常 为 了 验 证 本 文 所 提 出 的 谐 波 含 量 预 测 算
用的参数优化方法为群体智能算法，如灰狼优化 法 的 有 效 性 ，分 别 从 分 布 式 风 力 发 电 系 统 、
算法、遗传算法、粒子群算法、人工鱼群算法、麻雀 分 布 式 光 伏 发 电 系 统 以 及 储 能 系 统 的 采 样
算法等。本文选用了粒子群优化算法，该算法为
点 中 随 机 抽 取 采 样 时 间 为 30 s 的 数 据 进 行
全局寻优算法，且为并行寻优算法，具有收敛速度
验 证 。
快、寻优时间短、寻优精度高，以及不易陷入局部
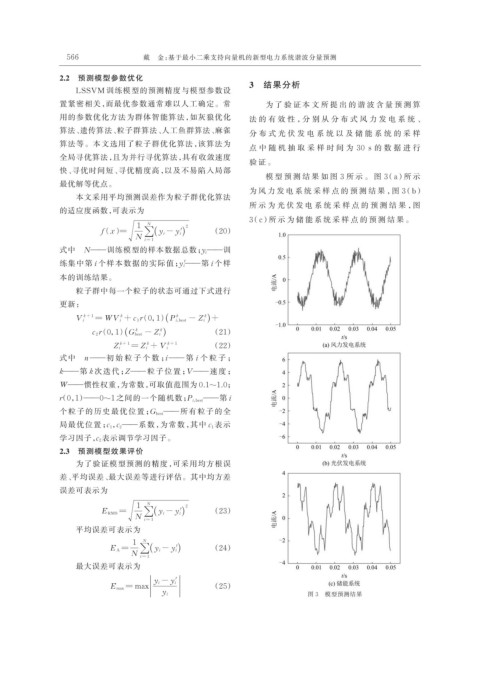
模 型 预 测 结 果 如 图 3 所 示 。 图 3（a）所 示
最优解等优点。
为 风 力 发 电 系 统 采 样 点 的 预 测 结 果 ，图 3（b）
本文采用平均预测误差作为粒子群优化算法
所 示 为 光 伏 发 电 系 统 采 样 点 的 预 测 结 果 ，图
的适应度函数，可表示为
3（c）所 示 为 储 能 系 统 采 样 点 的 预 测 结 果 。
1 N ) 2
f ( x )= ∑( y i - y ′ i （20）
N
i = 1
式中 N——训练模型的样本数据总数；y i——训
练集中第 i 个样本数据的实际值； y ′ i——第 i 个样

本的训练结果。
粒子群中每一个粒子的状态可通过下式进行
更新：
k + 1 k k k
V i = WV i + c 1 r ( 0，1 ) ( P i，best - Z i ) +
c 2 r ( 0，1 ) (G best - Z i ) （21）
k
k
k + 1 k k + 1
Z i = Z i + V i （22）
式中 n—— 初 始 粒 子 个 数 ；i—— 第 i 个 粒 子 ；
k——第 k 次迭代；Z——粒子位置；V——速度；
W——惯性权重，为常数，可取值范围为 0.1~1.0；
r（0，1） ——0~1 之间的一个随机数；P i，best——第 i
个粒子的历史最优位置；G best——所有粒子的全
c
局最优位置； 1，c 2——系数，为常数，其中 c 1 表示
c
学习因子， 2 表示调节学习因子。
2.3 预测模型效果评价
为了验证模型预测的精度，可采用均方根误

差、平均误差、最大误差等进行评估。其中均方差
误差可表示为
1 N ) 2
E RMS = ∑( y i - y ′ i （23）
N i = 1
平均误差可表示为
1 N )
E A = ∑( y i - y ′ i （24）
N
i = 1
最大误差可表示为
| | | y i - y ′ i | | |
E max = max| | | | （25）
| y i | 图 3 模型预测结果