Page 26 - 电力与能源2023年第四期

332 吴 迪，等：基于变异系数特征的配电网谐波责任评估方法

2 仿真验证

2.1 诺顿等效电路模型
参 照 文 献［5］在 MATLAB Simulink 中 建 立
诺顿等效电路模型进行仿真分析，以验证在用户
侧谐波阻抗非远大于系统侧谐波阻抗的情况下，

所提方法进行系统谐波阻抗估计的有效性。以 5
次谐波为测试对象，令 Z S=（10+j14） Ω，并考虑

由系统中新能源出力 ［20］ 、负荷变化等可能引起的
小幅度波动，在 Z S 的实部和虚部均添加 3% 的正
弦波动及 2% 的随机扰动；令|Z C|=a|Z S|，a 为实系
数，并考虑实际场景中 Z C 拥有较大波动，在其实
部和虚部均添加 5% 的正弦波动及 10% 的随机扰

动；用户侧发射谐波电流 İ C 的幅值设为 100 A，相
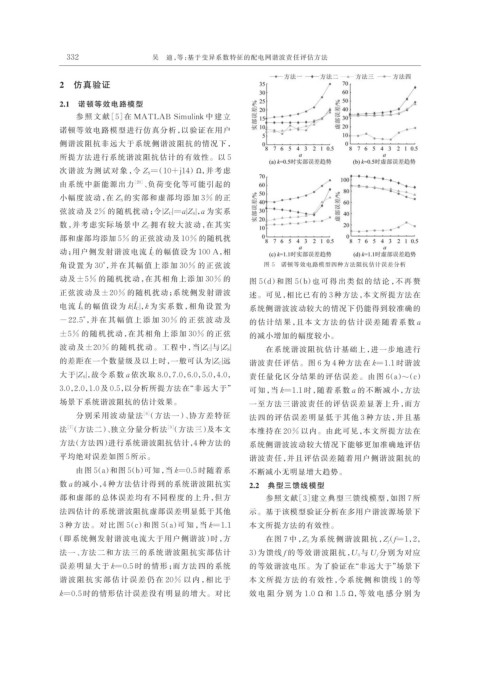
角设置为 30°，并在其幅值上添加 30% 的正弦波 图 5 诺顿等效电路模型四种方法阻抗估计误差分析
动及±5% 的随机扰动，在其相角上添加 30% 的 图 5（d）和 图 5（b）也 可 得 出 类 似 的 结 论 ，不 再 赘
正弦波动及±20% 的随机扰动；系统侧发射谐波 述。可见，相比已有的 3 种方法，本文所提方法在
电流 İ S 的幅值设为 k|İ C|，k 为实系数，相角设置为 系统侧谐波波动较大的情况下仍能得到较准确的
− 22.5°，并在其幅值上添加 30% 的正弦波动及 的估计结果，且本文方法的估计误差随着系数 a

±5% 的随机扰动，在其相角上添加 30% 的正弦 的减小增加的幅度较小。
波动及±20% 的随机扰动。工程中，当|Z C|与|Z S| 在系统谐波阻抗估计基础上，进一步地进行
的差距在一个数量级及以上时，一般可认为|Z C|远 谐波责任评估。图 6 为 4 种方法在 k=1.1 时谐波
大于|Z S|，故令系数 a 依次取 8.0，7.0，6.0，5.0，4.0， 责任量化区分结果的评估误差。由图 6（a）~（c）
3.0，2.0，1.0 及 0.5，以分析所提方法在“非远大于” 可知，当 k=1.1 时，随着系数 a 的不断减小，方法

场景下系统谐波阻抗的估计效果。 一至方法三谐波责任的评估误差显著上升，而方
［6］
分别采用波动量法 （方法一）、协方差特征 法四的评估误差明显低于其他 3 种方法，并且基
［9］
法 （方法二）、独立分量分析法 （方法三）及本文 本维持在 20% 以内。由此可见，本文所提方法在
［7］
方法（方法四）进行系统谐波阻抗估计，4 种方法的 系统侧谐波波动较大情况下能够更加准确地评估
平均绝对误差如图 5 所示。 谐波责任，并且评估误差随着用户侧谐波阻抗的
由图 5（a）和图 5（b）可知，当 k=0.5 时随着系 不断减小无明显增大趋势。

数 a 的减小，4 种方法估计得到的系统谐波阻抗实 2.2 典型三馈线模型
部和虚部的总体误差均有不同程度的上升，但方 参照文献［3］建立典型三馈线模型，如图 7 所
法四估计的系统谐波阻抗虚部误差明显低于其他 示。基于该模型验证分析在多用户谐波源场景下
3 种方法。对比图 5（c）和图 5（a）可知，当 k=1.1 本文所提方法的有效性。
（即系统侧发射谐波电流大于用户侧谐波）时，方 在图 7 中，Z 0 为系统侧谐波阻抗，Z f （f=1，2，

法一、方法二和方法三的系统谐波阻抗实部估计 3）为馈线 f 的等效谐波阻抗，U 0 与 U f 分别为对应
误差明显大于 k=0.5 时的情形；而方法四的系统 的等效谐波电压。为了验证在“非远大于”场景下
谐 波 阻 抗 实 部 估 计 误 差 仍 在 20% 以 内 ，相 比 于 本文所提方法的有效性，令系统侧和馈线 1 的等
k=0.5 时的情形估计误差没有明显的增大。对比 效 电 阻 分 别 为 1.0 Ω 和 1.5 Ω，等 效 电 感 分 别 为